质数

定义一个正整数 $p$ 为质数，即它不存在 $1$ 和 $p$ 以外的约数。$1$ 不是质数。

质数的判定

枚举法

可以枚举 $[1,\sqrt{n}]$ 中的整数，判定其是否为 $p$ 的约数。因为 $a \mid p$ 时 $\dfrac{p}{a}\mid p$，所以无需枚举到 $n$。复杂度为 $O(\sqrt{n})$。

:::info[实现]

这里给出一个 $\dfrac{1}{6}$ 常数的实现，筛掉 $2$ 和 $3$ 的倍数：

inline bool isprime(int x) {
	if (x <= 1) return false;
	if (x == 2 || x == 3) return true;
	if (x % 6 != 1 && x % 6 != 5) return false;
	for (int i = 5; i * i <= x; i += 6) {
		if (x % i == 0 || x % (i + 2) == 0) return false;
	}
	return true;
}

:::

Miller-Rabin 法

先引入二次探测定理，即：若 $p$ 为奇质数，则 $x^2 \equiv 1 \pmod p$ 的解为 $x \equiv 1$ 或 $x \equiv p-1$。

简证：由 $x^2 \equiv 1 \pmod p$ 得 $(x-1)(x+1) \equiv 0 \pmod p$，即可得出。

接下来使用费马小定理：若 $p$ 为质数且 $\gcd(a,p)=1$，则 $a^{p-1} \equiv 1 \pmod p$。这个结论的讲解可到文章下部。

设 $p-1=u \times 2^t$，随机一个 $a$ 值并求得 $v=a^u \bmod p$，然后执行 $t$ 次 $v \gets v^2 \bmod p$，检查是否满足 $a^{p-1} \equiv 1 \pmod p$。

在 long long 范围内，只需选取 $a \in \{2,325,9375,28178,450775,9780504,1795265022\}$ 即可保证正确性。复杂度 $O(\log n)$。

:::info[实现]

这里给出一个比较科技的写法。

inline long long power(long long a, long long b, long long p) {
	long long res = 1; for (a %= p; b; b >>= 1) {
		if (b & 1) res = (__int128) res * a % p;
		a = (__int128) a * a % p;
	} return res;
}

const long long BASE[] = {2, 325, 9375, 28178, 450775, 9780504, 1795265022};
inline bool miller_rabin(long long n) {
	if (n < 2 || n % 6 % 4 != 1) return (n | 1) == 3;
	long long s = __builtin_ctzll(n - 1), d = n >> s;
	for (long long a : BASE) {
		long long p = power(a, d, n), i = s;
		while (p != 1 && p != n - 1 && a % n && i--) p = (__int128) p * p % n;
		if (p != n - 1 && i != s) return false;
	} return true;
}

:::

威尔逊定理

若 $p$ 为质数，则

$$(p-1)! \equiv -1 \pmod p$$

其逆定理也成立。即若 $(p-1)! \equiv -1 \pmod p$，则 $p$ 为质数。

算术基本定理

任何一个合数 $n$ 可以唯一分解成有限个质数的乘积。

:::info[证明]

存在性：用反证法，假设 $n$ 是最小的不能被分解的合数，则存在 $n=ab$，若 $a,b$ 都可分解，则 $n$ 可以被分解；若 $a,b$ 有不可分解的数，则 $a,b$ 才是最小的数，矛盾。

唯一性：用反证法，假设 $n$ 是最小的存在两种分解的合数，如果 $n$ 存在两种分解 $n={p_1}^{a_1} {p_2}^{a_2} \cdots ={q_1}^{b_1} {q_2}^{b_2} \cdots$，则 $p_1 | {q_1}^{b_1} {q_2}^{b_2} \cdots$，也就是 ${q_1}^{b_1} {q_2}^{b_2} \cdots$ 中有一个 ${q_i}{b_i}$ 可以整除 $p_1$，故 $p_1=q_i$，同除 $p_1$，则 ${p_2}^{a_2} \cdots$ 也是存在两种分解的合数，矛盾。

:::

推论

设 $n$ 可以质因数分解为 $n=p_1^{c_1} p_2^{c_2} p_3^{c_3} \cdots p_m^{c_m}$。

推论 1：$n$ 的正约数个数为

$$(c_1+1)(c_2+1)(c_3+1)\cdots(c_m+1)=\prod_{i=1}^{m} (c_i+1) $$

推论 2：$n$ 的所有正约数和为

$$(1+p_1+p_1^2+\cdots+p_1^{c_1})\cdots(1+p_m+p_m^2+\cdots+p_m^{c_m})=\prod_{i=1}^{m} [\sum_{j=0}^{c_i} {p_i}^j] $$

分解质因数

试除法

与枚举法判素数同种原理，复杂度 $O(\sqrt{n})$。

:::info[实现]

int p[N], c[N];
int decompose(int n) {
	int m = 0;
	for (int i = 2; i * i <= n; i++) {
		if (n % i) continue;
		p[++m] = i, c[m] = 0;
		while (n % i == 0) n /= i, c[m]++;
	}
	if (n > 1) p[++m] = n, c[m] = 1;
	return m;
}

:::

需要注意的是，如果知道 $n$ 的值域，可以先用下面的质数筛打出一个质数表。由于质数平均隔 $O(\log n)$ 次出现一次，这样就省去了 $O(\log n)$ 次试除，故单次试除的复杂度降为 $O(\dfrac{\sqrt{n}}{\log n})$。

质数筛

埃氏筛

小学课本上学过，我们每遍历到一个质数，就把它的倍数划去，最后剩下的未被划去的就是质数。埃氏筛使用 bitset 优化后速度快于线性筛。

:::info[实现]

bitset<N> isprime;
void solve() {
	isprime.set(), isprime[0] = isprime[1] = false;
	for (int i = 2; i * i <= N; i++) {  // 一个常数优化：筛到 O(sqrt(N)) 即可
		if (!isprime[i]) continue;
		for (int j = 1LL * i * i; j < N; j += i) isprime[j] = false;
	}
}

:::

复杂度为 $O(n \log \log n)$。但是在实际计算中，bitset 优化后，它比 $O(n)$ 的线性筛更优秀。

线性筛

线性筛虽然跑不过 bitset 埃氏筛，但是它的思想值得学习。

埃氏筛复杂度到不了线性的原因是它会把一个合数划掉两遍。具体地，在标记 $i \times prime_j$ 时，需要确保 $i$ 的最小质因子不小于 $p$，即 $i\bmod prime_j =0$ 时跳出循环，这样复杂度就降到了 $O(n)$。

:::info[实现]

bitset<N> isprime;
int tot, prime[N];
void solve() {
	isprime.set(), isprime[0] = isprime[1] = false;
	for (int i = 2; i < N; i++) {
		if (isprime[i]) prime[++tot] = i;
		for (int j = 1; j <= tot; j++) {
			if (i * prime[j] >= N) break;
			isprime[i * prime[j]] = false;
			if (i & prime[j] == 0) break;
		}
	}
}

:::

区间筛

在一些题目中，我们可能需要求出 $[l,r]$ 中的质数，其中 $l,r \le 10^{14}$ 但 $r-l \le 10^7$。区间筛可在 $O(n \log \log n)$ 的时间复杂度内解决问题，其中 $n=\max(\sqrt{r},r-l)$。

观察到 $[l,r]$ 中的合数的最大质因数不会超过 $\sqrt{r}$，这意味着我们可以用埃氏筛先处理出 $[1,\sqrt{r}]$ 内的质数，再用这些质数去筛掉 $[l,r]$ 中的合数。这也就是埃氏筛那个常数优化的原理。

:::info[实现]

bitset<N> s, p;
void solve(int a, int b) {  // 筛出[a, b)之间的质数，用 p[i - a] 判断i是否为质数
	s.set(), p.set(), s[0] = s[1] = false;
	if (a <= 1) p[1 - a] = false;
	int z = (int) sqrt(b) + 1;
	for (int i = 2; i < z; i++) {
		for (int j = 2; i * j < z; j++) s[i * j] = false;
	}
	for (int i = 2; i * i <= b; i++) {
		if (!s[i]) continue;
		for (int j = max(i * i, (a + i - 1) / i * i); j < b; j += i) p[j - a] = false;
	}
}

:::

例题

P1147 连续自然数和

这种题型是一类常见题型，给出 $n$，并对于所求 $a,b$ 有 $ab=n$，则可以枚举 $n$ 的因数求解。

由等差数列求和：

$$\dfrac{(l+r)(r-l+1)}{2}=n$$

枚举 $2n=ij$，则

$$\left\{\begin{matrix} r-l+1=i\\ l+r=j \\ \end{matrix}\right. $$

解得

$$\left\{\begin{matrix} l=\dfrac{j-i+1}{2} \\ r=\dfrac{j+i-1}{2} \end{matrix}\right. $$

显然，$i,j$ 奇偶性应不同，且 $i$ 倒序枚举。复杂度 $O(\sqrt{n})$。

:::info[代码]

int n;
void _main() {
	cin >> n; n *= 2;
	for (int i = sqrt(n); i >= 2; i--) {
		if (n % i) continue;
		int j = n / i;
		if ((i & 1) + (j & 1) == 1) cout << (j - i + 1) / 2 << ' ' << (j + i - 1) / 2 << '\n';
	}
} 

:::

P1865 A % B Problem

由 $m \le 10^6$ 可以筛一下 $m$ 以内的质数，询问用前缀和处理。远古代码太丑了不想放。

P7960 [NOIP2021] 报数

质数筛的思想延伸。把含有 $7$ 的数先暴力找见，然后把它的倍数筛掉。

:::info[代码]

const int N = 1e7 + 1000;  // 注意这里要开大点
int t, x, nxt[N];
bitset<N> dis;

inline bool check(int x) {
	for (; x != 0; x /= 10) if (x % 10 == 7) return true;
	return false;
}

void _main() {
	int last = 0;
	dis.reset();
	for (int i = 1; i < N; i++) {
		if (dis[i]) continue;
		if (check(i)) {
			for (int j = 1; j * i < N; j++) dis[j * i] = 1;
			continue;
		}
		nxt[last] = i, last = i;
	}
	for (cin >> t; t--; ) {
		cin >> x;
		cout << (dis[x] ? -1 : nxt[x]) << '\n';
	}
}

:::

P1069 [NOIP 2009 普及组] 细胞分裂

形式化题意：给出 $m={m_1}^{m_2}$ 和 $n$ 个正整数 $a_i$，求

$$\min_{i \in [1,n]} \min_{m\mid a_i^k} k$$

显然这题 $m$ 不能给它算出来，对 $m_1$ 分解质因数，则

$$m={m_1}^{m_2}=(p_1^{c_1} p_2^{c_2} p_3^{c_3} \cdots p_h^{c_h})^{m_2}=p_1^{c_1m_2} p_2^{c_2m_2} p_3^{c_3m_2} \cdots p_h^{c_hm_2} $$

这样就得到了 $m$ 的质因数分解。对于每个 $a_i$，当且仅当 $\forall p_j, p_j \mid a_i$ 时有解，否则 $a_i$ 自乘多少次都不能使 $m$ 成为其约数。

接下来我们求出 $p_j$ 在 $a_i$ 中出现的次数 $cnt$。则对于 $p_j$ 而言，$\min k=\lceil \dfrac{c_j}{cnt} \rceil$。然后用木桶原理，对所有 $\min k$ 取 $\max$，为 $a_i$ 的答案。总复杂度 $O(n \sqrt{V})$，$V$ 是值域。

:::info[代码]

int n, m1, m2, a[N], tot;

int solve(int x) {
	int res = 0;
	for (int i = 1; i <= tot; i++) {
		if (x % p[i]) return INT_MAX;
		int cnt = 0;
		while (x % p[i] == 0) x /= p[i], cnt++;
		res = max(res, c[i] / cnt + (c[i] % cnt != 0));
	}
	return res;
}

void _main() {
	cin >> n >> m1 >> m2;
	for (int i = 1; i <= n; i++) cin >> a[i];
	tot = decompose(m1);  // 这个函数文章前面有
	for (int i = 1; i <= tot; i++) c[i] *= m2;
	int res = INT_MAX;
	for (int i = 1; i <= n; i++) res = min(res, solve(a[i]));
	cout << (res == INT_MAX ? -1 : res);
}

:::

AT_abc412_e [ABC412E] LCM Sequence

打个表可以发现，$A_n$ 发生变化当且仅当 $n$ 为质数或质数的幂。稍后证明此结论。然后我们用区间筛把质数筛出来，并且在筛法过程中处理质数的幂即可。注意 $A_l$ 贡献是单独的。还有一种方法是用 Miller-Rabin 判质数并且处理质数幂。

:::info[代码]

#define int long long
const int N = 1e7 + 5;
int l, r;
bitset<N> s, p;

void solve(int a, int b) {
	s.set(), p.set();
	int z = (int) sqrt(b) + 1;
	for (int i = 2; i < z; i++) {
		for (int j = 2; i * j < z; j++) s[i * j] = false;
	}
	for (int i = 2; i * i <= b; i++) {
		if (!s[i]) continue;
		for (int j = max(i * i, (a + i - 1) / i * i); j < b; j += i) p[j - a] = false;
	}
	for (int i = 2; i * i <= b; i++) {
		if (!s[i]) continue;
		int j = i * i;
		while (j < a) j *= i;
		for (; j < b; j *= i) p[j - a] = true;
	}
}

void _main() {
	cin >> l >> r;
	if (l == r) return cout << 1, void();
	solve(l, r + 1);
	int cnt = 0;
	for (int i = l; i <= r; i++) cnt += p[i - l];
	if (!p[0]) cnt++;
	cout << cnt;
}

:::

下面证明上述结论。由算术基本定理可设 $n={p_1}^{q_1}{p_2}^{q_2} \cdots {p_m}^{q_m}$。若 $m>1$，只要存在 ${{p_i}}^{q_i}$ 的倍数，$n$ 加入就不会改变 $\operatorname{lcm}$。而若 $m=1$，此时 $n={p_1}^{q_1}>n-1$，此时 $n$ 为质数幂。

最大公约数

求解 GCD

STL

C++ STL 中有函数 std::__gcd，为迭代的辗转相除法实现，复杂度为 $O(\log n)$，可以直接使用。

分解质因数法

将两数分解质因数：$a=p_1^{a_1}p_2^{a_2} \cdots, b=a=p_1^{b_1}p_2^{b_2} \cdots$，则 $\gcd(a,b)=p_1^{\min(a_1,b_1)}p_2^{\min(a_2,b_2)} \cdots$，复杂度为 $O(\sqrt{n})$。

这证明：求 gcd 和求最小值有共通之处。

辗转相除法

GCD 有如下性质：

$$\gcd(a,b)=\gcd(b,a \bmod b)$$

利用此可递归计算 gcd，出口为 $\gcd(a,0)=a$。复杂度 $O(\log (a+b))$。

:::info[实现]

int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}

:::

更相减损法

GCD 有如下性质：

$$\gcd(a,b)=\gcd(a-b,b)$$

如果直接递归计算，复杂度为 $O(n)$。Stein 算法对此进行了优化：

若 $2\mid a$ 且 $2\mid b$，则 $\gcd(a,b)=2\gcd(\dfrac{a}{2},\dfrac{b}{2})$。而若只有 $2 \mid a$，则 $\gcd(a,b)=\gcd(\dfrac{a}{2},b)$。这启示我们可以在过程中除掉约数 $2$，复杂度降到了 $O(\log n)$。Stein 算法常用于大整数的 GCD。

Stein 算法可以借助二进制内置函数优化，称作 Binary GCD，理论复杂度 $O(\log (a+b))$，但在实际表现中可以看作大常数 $O(1)$。

:::info[实现]

这份代码的速度比 std::__gcd 更快，可以卡过 P5435。

constexpr int gcd(int a, int b) {
	int az = __builtin_ctz(a), bz = __builtin_ctz(b), z = min(az, bz);
	b >>= bz;
	while (a) {
		a >>= az;
		int d = a - b;
		az = __builtin_ctz(d);
		b = min(a, b), a = abs(d);
	}
	return b << z;
}

:::

exGCD

exGCD 用于求解形如 $ax+by=\gcd(a,b)$ 一类的不定方程。

裴蜀定理

对于任意非零整数 $a,b$，$ax+by=c$ 有整数解当且仅当 $c \mid \gcd(a,b)$。

推论

若 $a_1,a_2,a_3,\cdots,a_n$ 是不全为 $0$ 的整数，则存在整数 $x_1,x_2,x_3,\cdots,x_n$ 使得

$$a_1x_1+a_2x_2+a_3x_3+\cdots+a_nx_n=\gcd(a_1,a_2,a_3,\cdots,a_n) $$

其逆定理也成立。

不定方程

由 $\gcd(a,b)=\gcd(b,a\bmod b)$ 得：

$$\begin{aligned} ax+by&=bx'+(a\bmod b)y'\\ &=bx'+(a-b\lfloor \dfrac{a}{b} \rfloor)y'\\ &=ay'+b(x'-y'\lfloor \dfrac{a}{b} \rfloor) \end{aligned} $$

递归式：$x=y',y=x'-y'\lfloor \dfrac{a}{b} \rfloor$，这样就可以 $O(\log (a+b))$ 求解。

:::info[实现]

void exgcd(int a, int b, int& x, int& y) {
	if (b == 0) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}

:::

乘法逆元

逆元就是模意义下的倒数：求 $x \equiv \dfrac{1}{a} \pmod m$ 的解。

移项得：$ax \equiv 1 \pmod m$，即为求解不定方程 $ax-bm=1$，用 exGCD 求解即可。

这里可以发现，$x$ 在模 $m$ 意义下有逆元当且仅当 $x,m$ 互质。利用乘法逆元，可以实现模意义下的除法。

线性方程组

这里的线性方程组是指求一个最小的 $x$ 满足

$$\left\{\begin{matrix} x \equiv a_1 \pmod {m_1} \\ x \equiv a_2 \pmod {m_2} \\ \cdots \\ x \equiv a_n \pmod {m_n} \end{matrix}\right. $$

两两考虑。比如我们把前两个方程变成不定方程：$x=m_1p+a_1=m_2q+a_2$。则 $m_1p-m_2q=a_2-a_1$，利用 exGCD 解出一组可行解 $(p,q)$，然后这两个方程组的共同解为 $x \equiv (m_1p+a_1) \pmod {\operatorname{lcm}(m_1,m_2)}$。然后把 $n$ 个方程都这么合并起来即可。

至于为什么不说 CRT，因为我觉得 exCRT 比 CRT 更容易理解，适用范围更广，代码还好写。

例题

P1072 [NOIP 2009 提高组] Hankson 的趣味题

有一个结论：若 $\gcd(a,b)=c$，且 $a=k_1c,b=k_2c$，则 $\gcd(k_1,k_2)=1$。

证明：考虑反证法，设 $K=\gcd(k_1,k_2) \ne 1$，则存在不为 $1$ 的正整数 $p,q$ 使得 $k_1=pK,k_2=qK$，因而 $a=pKc,b=qKc$，$\gcd(a,b)=Kc \ne c$，故原结论成立。

由题可得：$x=a_1 p$，$b_1=xq$，其中 $p,q$ 为正整数。

由上述结论得：$\gcd(\dfrac{a_0}{a_1},\dfrac{x}{a_1})=1$。又有 $\operatorname{lcm}(x,b_0)=b_1$，故 $\gcd(\dfrac{b_1}{x},\dfrac{b_1}{b_0})=1$。且 $x\mid b_1$，枚举 $x$ 并判断即可，复杂度 $O(\sqrt{b_1} \log V)$。

:::info[代码]

int a0, a1, b0, b1;

void _main() {
	cin >> a0 >> a1 >> b0 >> b1;
	int cnt = 0;
	for (int x = 1; x * x <= b1; x++) {
		if (b1 % x) continue;
		if (x % a1 == 0 && __gcd(x / a1, a0 / a1) == 1 && __gcd(b1 / x, b1 / b0) == 1) cnt++;
		int y = b1 / x;
		if (x == y) continue;
		if (y % a1 == 0 && __gcd(y / a1, a0 / a1) == 1 && __gcd(b1 / y, b1 / b0) == 1) cnt++;
	}
	cout << cnt << '\n';
}

:::

P4549 【模板】裴蜀定理

由 $\gcd(a,b,c)=\gcd(a,\gcd(b, c))$ 和裴蜀定理得

$$\sum_{i=1}^{n} a_i x_i = \gcd_{i=1}^{n} |a_i|$$

而题目中记 $\sum x_i$ 为 $S$，可知 $\gcd_{i=1}^{n} |a_i|$ 是 $S$ 的约数，$S$ 最小时二者相等。也就是求所有数的 $\gcd$。

:::info[代码]

int n, res, a;
int main() {   // 两年前的马蜂
    scanf("%d", &n);
    while (n--) scanf("%d", &a), a = abs(a), res = __gcd(res, a);
    printf("%d", res);
    return 0;
}

:::

CF510D Fox And Jumping

根据裴蜀定理的推论，能跳到所有位置当且仅当我们选出的长度的 $\gcd=1$。于是设 $dp_i$ 表示选择一些长度使得其最大公约数为 $i$ 的最小代价，采用刷表，枚举 $i,j \in [1,n]$ 易得

$$dp_{\gcd(l_i, j)} \gets \min(dp_{\gcd(l_i, j)}, c_{i}+v) $$

对于单个转移，有

$$dp_{l_i} \gets \min(dp_{l_i},c_i)$$

由于下标能到 $10^9$，暴力 dp 是不行的。但是有用的 $dp$ 值不多，于是我们用 std::map 维护转移，复杂度比较玄学。

:::info[代码]

const int N = 305;
int n, l[N], c[N];
map<int, int> dp;
void upd(int x, int v) {
	if (!dp.count(x)) dp[x] = v;
	else dp[x] = min(dp[x], v);
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> l[i];
	for (int i = 1; i <= n; i++) cin >> c[i];
	for (int i = 1; i <= n; i++) {
		for (const auto& h : dp) {
			int j = h.first, v = h.second;
			upd(__gcd(l[i], j), c[i] + v);
		} upd(l[i], c[i]);
	}
	cout << (dp.count(1) ? dp[1] : -1);
}

:::

P1082 [NOIP 2012 提高组] 同余方程

这东西我们在之前的乘法逆元讲过方法了，就是用 exGCD 解方程 $ax-by=1$。输入保证有解，意味着 $\gcd(a,b)=1$，所以这就是 exGCD 方程的标准形式。细节上，求出 $x$ 以后要处理负数问题。

:::info[代码]

template <class T> void exgcd(T a, T b, T& x, T& y) {
	if (b == 0) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}

long long a, b;
void _main() {
	cin >> a >> b;
	long long x, y; exgcd(a, b, x, y);
	cout << (x % b + b) % b;
}

:::

P5656 【模板】二元一次不定方程 (exgcd)

首先由裴蜀定理判无解，若 $c$ 不是 $\gcd(a,b)$ 的倍数则直接无解。

设 $\gcd(a,b)=d$。考虑用 exGCD 求解方程 $ax+by=d$，将解记作 $x_0,y_0$。则

$$ax_0+by_0=d\\$$

方程两边同乘 $\dfrac{c}{d}$ 转化为所求：

$$a\dfrac{cx_0}{d}+b\dfrac{cy_0}{d}=c\\$$

故原方程的一组解为 $x_1=\dfrac{cx_0}{d},y_1=\dfrac{cy_0}{d}$。

接下来考虑构造通解形式，设

$$a(x_1+m)+b(y_0+n)=c$$

不难发现 $m,n$ 满足条件 $am+bn=0$。仍然利用裴蜀定理，解得 $m=p \times \dfrac{b}{d}, n=-p \times {a}{d}$，其中 $p$ 是正整数。于是我们得到原方程的通解

$$\left\{\begin{matrix} x=x_1+p \times \dfrac{b}{d} \\ y=y_1-p \times \dfrac{a}{d} \end{matrix}\right. $$

考虑求解数与最值。找 $x_{\min}$ 即为解关于 $k$ 的不等式

$$x_1+km \ge 1$$

由于式中的值均为整数，故

$$k \ge \lceil \dfrac{1-x_1}{m} \rceil$$

由于 $y$ 随 $x$ 的增大而减小，故 $x_{\min}$ 所对应的 $y$ 就是 $y_{\max}$。接下来我们用 $y_{\max}$ 推 $y_{\min}$。推导一下，可以发现

$$y_{\min}=y_{\max} \bmod n$$

于是 $x_{\max}$ 加上同样多的 $m$ 即可：

$$x_{\max}=x_{\min} + \lfloor \dfrac{y_{\max}-1}{n} \times m \rfloor $$

解数就是 $[y_{\min},y_{\max}]$ 中解的个数，即

$$\lfloor \dfrac{y_{\max}-1}{n} +1 \rfloor$$

至此本题在 $O(\log V)$ 内解决，$V$ 为值域。

在实现中，我们可以将 $a,b,c$ 都除去 $d$，这样可以简化代码。

:::info[代码]

template <class T> void exgcd(T a, T b, T& x, T& y) {
	if (b == 0) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}

long long a, b, c;

void _main() {
	cin >> a >> b >> c;
	long long d = __gcd(a, b);
	if (c % d) return cout << -1 << '\n', void();
	a /= d, b /= d, c /= d;
	long long x0, y0; exgcd(a, b, x0, y0);
	long long x1 = c * x0, y1 = c * y0;
	int xmin = (x1 > 0 && x1 % b != 0) ? x1 % b : x1 % b + b;
	int ymax = (c - xmin * a) / b;
	int ymin = (y1 > 0 && y1 % a != 0) ? y1 % a : y1 % a + a;
	int xmax = (c - ymin * b) / a;
	if (xmax <= 0) cout << xmin << ' ' << ymin << '\n';
	else cout << (ymax - ymin) / a + 1 << ' ' << xmin << ' ' << ymin << ' ' << xmax << ' ' << ymax << ' ' << '\n';
}

:::

P1516 青蛙的约会

设相遇时两只青蛙跳了 $t$ 次，则

$$(n-m)t+kL=x-y$$

即求解 $t$ 的最小非负整数解。在不定方程 $ax+by=c$ 中，我们把 $n-m$ 视作 $a$，$L$ 视作 $b$，$x-y$ 视作 $c$，则应用上一题的方法来求解。

:::info[代码]

template <class T> void exgcd(T a, T b, T& x, T& y) {
	if (b == 0) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
long long x, y, m, n, L;

void _main() {
	cin >> x >> y >> m >> n >> L;
	long long a = n - m, b = L, c = x - y;
	if (a < 0) a = -a, c = -c;
	long long d = __gcd(a, b);
	if (c % d) return cout << "Impossible", void();
	a /= d, b /= d, c /= d;
	long long x0, y0; exgcd(a, b, x0, y0);
	long long x1 = c * x0;
	cout << ((x1 > 0 && x1 % b != 0) ? x1 % b : x1 % b + b);
}

:::

P4777 【模板】扩展中国剩余定理（EXCRT）

这种解线性方程组的方法一般称作 exCRT。套用上面的 exGCD 法即可。

:::info[代码]

const int N = 1e5 + 5;

template <class T> void exgcd(T a, T b, T& x, T& y) {
	if (!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
template <class T> T crt(int n, const T* a, const T* m) {
	T x = 0, y = 0, p = m[1], res = a[1];
	for (int i = 2; i <= n; i++) {
		T a0 = p, b0 = m[i], c = (a[i] - res % b0 + b0) % b0, g = __gcd(a0, b0);
		if (c % g) return -1;
		exgcd(a0, b0, x, y);
		x = (__int128) x * c / g % b0, res += x * p, p = p / __gcd(p, b0) * b0, res = (res % p + p) % p;
	}
	return res;
}

int n;
long long a[N], m[N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> m[i] >> a[i];
	cout << crt(n, a, m);
}

:::

exCRT 很重要的一个用途是对于模数不是质数的情况，我们把模数分解质因数，然后分别计算对这些质因数取模的结果，最后用 exCRT 合并。

P3868 [TJOI2009] 猜数字

对于 $(x-a_i) \mid b_i$，可以变形为 $x-a_i \equiv 0 \pmod {b_i}$，然后再移项就是 $x \equiv a_i \pmod {b_i}$。于是解这个同余方程组即可。

细节上注意 $a_i$ 可能为负，需要对 $b_i$ 取模处理，另外这题会爆 long long，不过上面板子里已经开了 __int128 了。

:::info[代码]

const int N = 15;
int n;
long long a[N], b[N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];
	for (int i = 1; i <= n; i++) a[i] = (a[i] % b[i] + b[i]) % b[i];
	cout << crt(n, a, b);
}

:::

欧拉函数

定义

欧拉函数 $\varphi(x)$ 指 $[1,n]$ 中与 $n$ 互质的数的个数。

若由算术基本定理可将 $n$ 分解为 $p_1^{c_1} p_2^{c_2} p_3^{c_3} \cdots p_m^{c_m}$，则

$$\varphi(x)=n (1-\dfrac{1}{p_1}) (1-\dfrac{1}{p_2}) (1-\dfrac{1}{p_3}) \cdots (1-\dfrac{1}{p_m}) =n\times \prod_{i=1}^{m} (1-\dfrac{1}{p_i}) $$

由此有一个 $O(\sqrt{n})$ 计算欧拉函数的方法：

:::info[实现]

inline int phi(int n) {
	if (n == 1) return 1;
	int res = n;
	for (int i = 2; i * i <= n; i++) {
		if (n % i == 0) {
			res = res / i * (i - 1);
			while (n % i == 0) n /= i;
		}
	}
	if (n > 1) res = res / n * (n - 1);
	return res;
}

:::

性质

性质 1：若 $p$ 是质数，则 $\varphi(p)=p-1$。

性质 2：若 $a,b$ 互质，则 $\varphi(ab)=\varphi(a) \times \varphi(b)$。这表明：欧拉函数是积性函数，因而可以用线性筛筛出。

性质 3：$\sum_{d \mid n} \varphi(d)=n$。

性质 4：对于 $n>1$，$[1,n]$ 中与 $n$ 互质的数的和为 $\dfrac{1}{2}n\times \varphi(n)$。

性质 5：若 $n=p^k$，其中 $p$ 是质数，则 $\varphi(n)=p^k-p^{k-1}$。

筛法

使用性质 2 并结合线性筛法，可以在 $O(n)$ 时间内预处理 $[1,n]$ 的欧拉函数值。

:::info[实现]

int len, phi[N], prime[N];
bitset<N> isprime;

inline void eular(int n) {
	phi[1] = 1, isprime.set(), isprime[0] = isprime[1] = false;
	for (int i = 2; i <= n; i++) {
		if (isprime[i]) prime[++len] = i, phi[i] = i - 1;
		for (int j = 1; j <= len && i * prime[j] <= n; j++) {
			isprime[i * prime[j]] = false;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * phi[prime[j]];
		}
	}
}

:::

例题

SP4141 ETF - Euler Totient Function

线性筛欧拉函数板子。

:::info[代码]

const int N = 1e6 + 5;
void _main() {
	eular(N - 1);
	int t, x; cin >> t;
	while (t--) cin >> x, cout << phi[x] << '\n';
}

:::

UVA10179 Irreducable Basic Fractions

题意翻译：求 $\dfrac{0}{n},\dfrac{1}{n},\dfrac{2}{n},\cdots \dfrac{n-1}{n}$ 中多少个分数为最简分数。认为 $\dfrac{0}{n}$ 最简。

我们发现最简分数 $\dfrac{x}{n}$ 满足 $\gcd(x,n)=1$，于是所求为 $\varphi(n)$。用分解质因数法求即可，代码不放了。

P2158 [SDOI2008] 仪仗队

由样例图可以发现能看见的位置关于对角线对称，只需要考虑一个三角形即可。以左下角为原点 $(0,0)$ 建立坐标系，则一个点被阻挡的条件就是到原点连线的斜率相同。设两点 $(x_1,y_1),(x_2,y_2)$，则 $\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}$。当且仅当这个分数已经为最简形式时它不会被挡住，这就和上题类似了。

所求即为

$$2\sum_{i=1}^{n-1} \varphi(i)+1$$

这是因为 $(2,2)$ 满足条件而我们无法统计进去。注意特判 $n=1$。

用线性筛筛出欧拉函数即可，复杂度 $O(n)$。

:::info[代码]

int n;
void _main() {
	cin >> n;
	if (n == 1) return cout << 0, 0;
	int res = 1;
	eular(40000);
	for (int i = 1; i < n; i++) res += 2 * phi[i];
	cout << res;
}

:::

P2398 GCD SUM

这题做法很多，读者可以翻到下文容斥例题学习容斥做法，这里写的是欧拉函数做法。

可以发现 $\gcd(i,j)$ 的值只有 $n$ 种，不妨考虑 $gcd(i,j)=k$ 的数目。对于一对互质的 $i,j$，有 $\gcd(ik,jk)=k$，所以可以得到结果为 $k$ 的数目为

$$2\sum_{i=1}^{\lfloor \frac{n}{k} \rfloor} \varphi(i)-1 $$

和上面那题是一样的，因为 $\gcd(i,j)=\gcd(j,i)$ 有对称性，而 $(1,1)$ 会重复计算，要减一。

然后我们用线性筛处理出 $\varphi(i)$ 的前缀和，$O(n)$ 计算即可。

:::info[代码]

const int N = 1e5 + 5;
int n;
long long pre[N];

void _main() {
	cin >> n;
	eular(n);
	for (int i = 1; i <= n; i++) pre[i] = pre[i - 1] + phi[i];
	long long res = 0;
	for (int i = 1; i <= n; i++) res += 1LL * i * (2 * pre[n / i] - 1);
	cout << res;
}

:::

双倍经验：P1390。这个题没有对称性，把系数 $2$ 去掉即可。

数论常用定理

费马小定理

若 $p$ 为质数，且 $\gcd(a,p)=1$，则 $a^{p-1} \equiv 1 \pmod p$。

变形式：$a^p\equiv a \pmod p$ 和 $a^{p-2}\equiv \dfrac{1}{a} \pmod p$。其中第二个式子表明，当 $p$ 为质数时可以直接用快速幂求逆元。

:::success[证明]

取一个不为 $p$ 的倍数的数 $a$，构造序列 $A=\{1,2,3, \cdots p-1\}$，则：

$$\prod_{i=1}^{p-1} A_i \equiv \prod_{i=1}^{p-1} (A_i\times a) \pmod p $$

考虑每一个 $A_i$ 都不是 $p$ 的约数易证。则令 $m=(p-1)!$，则

$$m \equiv \prod_{i=1}^{p-1} (A_i\times a) \pmod p$$

又有 $a^{p-1} \times f \equiv f \pmod p$，故

$$a^{p-1} \equiv 1 \pmod p$$

:::

欧拉定理

欧拉定理是费马小定理的扩展形式。若 $\gcd(a,n)=1$，则 $a^{\varphi(n)} \equiv 1 \pmod n$。证明与费马小定理类似，构造一个与 $n$ 互质的序列即可。

推论

推论 1：若 $\gcd(a,n)=1$，则 $a^b \equiv a^{b \bmod \varphi(n)} \pmod n$。

推论 2：若 $\gcd(a,n)=1$，则满足 $a^x \equiv 1 \pmod n$ 的最小正整数是 $\varphi(n)$ 的约数。

扩展欧拉定理

扩展欧拉定理在 OI 中常用于对幂取模的情况。

$$a^b \equiv \left\{\begin{matrix} a^{b \bmod \varphi(n)} & \gcd(a,n)=1 \\ a^b & \gcd(a,n) \ne 1,b < \varphi(n) \\ a^{(b \bmod \varphi(n))+\varphi(n)} & \gcd(a,n) \ne 1, b \ge \varphi(n) \end{matrix}\right. \pmod n $$

例题

P4139 上帝与集合的正确用法

题里给的那个东西实际上是 $2^{2^{2^{2^ \cdots}}} \bmod p$。对指数塔不断递归，用扩展欧拉定理降幂即可。$\varphi(n)$ 提前筛出来。

由于指数塔是无限层，因此肯定有 $b \ge \varphi(n)$，直接认为是第三种情况就行了。

:::info[代码]

long long p;
long long power(long long a, long long b, long long p) {
	long long res = 1; for (a %= p; b; a = a * a % p, b >>= 1) {
		if (b & 1) res = res * a % p;
	} return res;
}
long long f(long long p) {return p == 1 ? 0 : power(2, f(phi[p]) + phi[p], p);}

void _main() {   // 这里已经筛过phi[n]了
	cin >> p; cout << f(p) << '\n';
}

:::

P10496 The Luckiest Number

设答案为 $x$ 个 $8$ 连在一起的整数 $n$，由等比数列求和

$$\begin{aligned} n&=8+8\times 10+8\times 10^2 + \cdots + 8 \times 10^x\\ &=\sum_{i=0}^{x} 8 \times 10^i \\ &=\dfrac{8(10^x-1)}{9} \end{aligned} $$

设 $d=\gcd(L,8)$，则由题知 $L \mid \dfrac{8(10^x-1)}{9}$，故 $9L \mid 8(10^x-1)$，即

$$\dfrac{9L}{d} \mid (10^x-1)$$

因此，$10^ x \equiv 1 \pmod {\dfrac{9L}{d}}$。

由欧拉定理的推论 2，我们求出 $\varphi(\dfrac{9L}{d})$ 并枚举其约数检查即可，复杂度 $O(\sqrt{L} \log L)$。

:::info[代码]

long long power(long long a, long long b, long long p) {
	long long res = 1; for (a %= p; b; a = (__int128) a * a % p, b >>= 1) {
		if (b & 1) res = (__int128) res * a % p;
	} return res;
}
vector<long long> factors(long long n) {
	vector<long long> res;
	for (long long i = 1; i * i <= n; i++) {
		if (n % i) continue;
		res.emplace_back(i);
		if (n / i != i) res.emplace_back(n / i);
	}
	sort(res.begin(), res.end());
	return res;
}

long long n;

void _main() {
	for (int kase = 1; ; kase++) {
		cin >> n;
		if (n == 0) break;
		cout << "Case " << kase << ": ";
		n = 9 * n / __gcd(n, 8LL);
		if (__gcd(n, 10LL) != 1) {cout << "0\n"; continue;}
		vector<long long> f = factors(phi(n));
		for (long long x : f) {
			if (power(10, x, n) == 1) {cout << x << '\n'; break;}
		}
	}
}

:::

P2480 [SDOI2010] 古代猪文

我们先形式化题意，就是要求

$$g^{\sum_{d \mid n} C_n^d} \bmod 999911659$$

首先你打个 $O(\sqrt{n})$ 判质数，发现 $999911659$ 是质数，由欧拉定理的推论 1

$$g^{\sum_{d \mid n} C_n^d} \equiv g^{\sum_{d \mid n} C_n^d \bmod \varphi(999911659)} \pmod {999911659} $$

由欧拉函数性质 1，$\varphi(999911659)=999911659-1=999911658$，因此

$$g^{\sum_{d \mid n} C_n^d} \equiv g^{\sum_{d \mid n} C_n^d \bmod 999911658} \pmod {999911659} $$

所以只需求 $\sum_{d \mid n} C_n^d \bmod 999911658$ 然后快速幂即可。如果直接上 exLucas，复杂度会爆炸，考虑怎么做。我们打一个 $O(\sqrt{n})$ 试除法分解质因数可得

$$999911658=2\times 3 \times 4679 \times 35617$$

用 $O(\sqrt{n})$ 枚举 $d \mid n$，然后使用 Lucas 定理计算 $C^{d}_n$ 对 $2,3,4679,35617$ 取模的结果，然后 exCRT 合并答案即可。如果你还不会 Lucas 定理求组合数，请移步下文学习后再看代码。

:::warning[注意]

欧拉定理成立的条件是 $\gcd(g,999911659)=1$，若不成立要判无解，以及 exCRT 也要判无解。

:::

:::info[代码]

#define int long long
int n, g;

int power(int a, int b, int p) {
	int res = 1; for (a %= p; b; b >>= 1) {
		if (b & 1) res = res * a % p;
		a = a * a % p;
	} return res;
}

namespace Lucas {
	int fac[N], ifac[N];
	inline void init(int p) {
		fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
		for (int i = 2; i <= p; i++) fac[i] = fac[i - 1] * i % p, ifac[i] = power(fac[i], p - 2, p);
	} inline int C(int n, int m, int p) {
		if (n < m) return 0;
		return fac[n] * ifac[m] % p * ifac[n - m] % p; 
	} int lucas(int n, int m, int p) {
		if (m == 0) return 1;
		if (n < p && m < p) return C(n, m, p);
		return lucas(n / p, m / p, p) * C(n % p, m % p, p) % p;
	}
}

namespace CRT {
	template <class T> void exgcd(T a, T b, T& x, T& y) {
		if (!b) return x = 1, y = 0, void();
		exgcd(b, a % b, y, x), y -= a / b * x;
	}
	template <class T> T crt(int n, const T* a, const T* m) {
		T x = 0, y = 0, p = m[1], res = a[1];
		for (int i = 2; i <= n; i++) {
			T a0 = p, b0 = m[i], c = (a[i] - res % b0 + b0) % b0, g = __gcd(a0, b0);
			if (c % g) return -1;
			exgcd(a0, b0, x, y);
			x = (__int128) x * c / g % b0, res += x * p, p = p / __gcd(p, b0) * b0, res = (res % p + p) % p;
		}
		return res;
	}
}

const int P[] = {0, 2, 3, 4679, 35617};
int a[5];

void _main() {
	cin >> n >> g;
	if (__gcd(g, 999911659LL) != 1) return cout << 0, void();  // 注意判无解
	for (int i = 1; i <= 4; i++) {
		Lucas::init(P[i]);
		for (int d = 1; d * d <= n; d++) {
			if (n % d) continue;
			a[i] = (a[i] + Lucas::lucas(n, d, P[i])) % P[i];
			if (n / d != d) a[i] = (a[i] + Lucas::lucas(n, n / d, P[i])) % P[i];
		} 
	} 
	int val = CRT::crt(4, a, P);
	if (val == -1) return cout << 0, void();  // 注意判无解
	cout << power(g, val, 999911659);
} 

:::

这个题基本把我们讲过的数论知识都用了一遍，是一道很全面很综合的好题。

数论分块

数论分块用于快速计算形如

$$\sum_{i=1}^{n} f(i) g(\lfloor \dfrac{k}{i} \rfloor) $$

的式子，其中 $f(i)$ 可处理出前缀和或可以快速计算 $f(x)-f(y)$。如果这是 $O(1)$ 的，则数论分块可在 $O(\sqrt{n})$ 的时间内得出结果。

原理

以函数 $y=\lfloor \dfrac{100}{x} \rfloor$ 为例，图像如下：

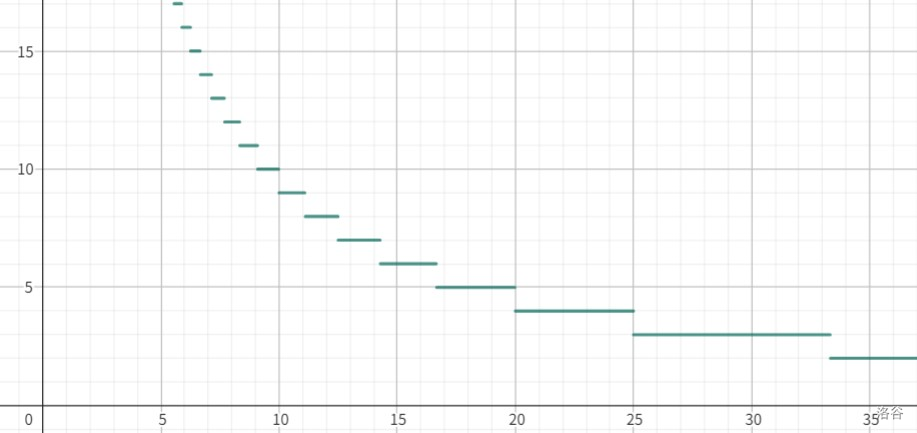
我们注意到对于每个固定的 $y$，$x$ 的取值总是一个固定区间。事实上，$\lfloor \dfrac{k}{i} \rfloor$ 不变时，$i \le \lfloor \frac{k}{\lfloor \frac{k}{i} \rfloor} \rfloor$。

:::success[证明]

设 $m=\lfloor \dfrac{k}{i} \rfloor$，则 $m \le \dfrac{k}{i}$，所以 $\lfloor \dfrac{k}{m} \rfloor \ge \lfloor \frac{k}{\frac{k}{i}} \rfloor=i$。

因此，$i_{\max}=\lfloor \dfrac{k}{m} \rfloor=\lfloor \frac{k}{\lfloor \frac{k}{i} \rfloor} \rfloor$。

:::

板子

template <class F_t, class G_t>
long long sqrt_decomposition(long long n, long long k, F_t f, G_t g) {
	long long res = 0;
	for (long long l = 1, r = 0; l <= n; l = r + 1) {
		r = (k / l) ? min(n, (k / (k / l))) : n;
		res += f(r, l - 1) * g(k / l);
	}
	return res;
}

这个板子第一个参数传入 $n$，第二个参数传入 $k$，第三个参数传入一个函数计算 $f(x)-f(y)$，第四个参数传入 $g(x)$ 的函数。

例题

UVA11526 H(n)

【模板】数论分块。

:::info[代码]

int n;
void _main() {
	cin >> n;
	cout << sqrt_decomposition(n, n,
		[](long long x, long long y) {return x - y;}, // f(x) = 1
		[](long long x) {return x;} // g(x) = x
	) << '\n';
}

:::

P2424 约数和

首先考虑求 $f(x)$ 的前缀和 $g(x)$。有一个结论是 $i$ 的约数在 $n$ 以内有 $\lfloor \dfrac{n}{i} \rfloor$ 个，所以

$$g(x) = \sum_{i=1}^{n} i \times \lfloor \dfrac{n}{i} \rfloor $$

然后套板子去求即可。

:::info[代码]

long long g(long long n) {
	if (n <= 1) return n;
	return sqrt_decomposition(n, n, 
		[](long long x, long long y) {return (x - y) * (x + y + 1) / 2;},
		[](long long x) {return x;}
	);
}

long long l, r;
void _main() {
	cin >> l >> r;
	cout << g(r) - g(l - 1);
}

:::

P2261 [CQOI2007] 余数求和

根据取模的定义，有 $a \bmod b=a-b \times \lfloor \dfrac{a}{b} \rfloor$，然后推一波式子：

$$\begin{aligned} G(n, k) &= \sum_{i = 1}^n k \bmod i \\ &= \sum_{i = 1}^n k -i \times \lfloor \dfrac{k}{b} \rfloor \\ &= nk-\sum_{i = 1}^n i \times \lfloor \dfrac{k}{b} \rfloor \end{aligned} $$

后面这个东西可以数论分块来做。

:::info[代码]

long long n, k;

void _main() {
	cin >> n >> k;
	cout << n * k - sqrt_decomposition(n, k, 
		[](long long x, long long y) {return (x - y) * (x + y + 1) / 2;}, // f(x) = x
		[](long long x) {return x;} // g(x) = x
	);
}

:::

P2260 [清华集训 2012] 模积和

和上面的题很像。

推柿子：

$$\begin{aligned} ans &=\sum_{i=1}^{n} \sum_{j=1}^{m} (n \bmod i) \times (m \bmod j), i \neq j \\ &=\sum_{i=1}^{n} \sum_{j=1}^{m} (n \bmod i) \times (m \bmod j)-\sum_{i=1}^{\min(n,m)} (n \bmod i) \times (m \bmod i)\\ &=\sum_{i=1}^n(n-\lfloor\frac{n}{i}\rfloor\times i)\times\sum_{j=1}^m(m-\lfloor\frac{m}{j}\rfloor\times j)-\sum_{i=1}^{\min(n,m)}(n-\lfloor\frac{n}{i}\rfloor\times i)\times(m-\lfloor\frac{m}{i}\rfloor\times i)\\ &=(n^2-\sum_{i=1}^ni\times\lfloor\frac{n}{i}\rfloor)\times(m^2-\sum_{i=1}^mi\times\lfloor\frac{m}{i}\rfloor)-\sum_{i=1}^{\min(n,m)}(nm-mi\times\lfloor\frac{n}{i}\rfloor-ni\times\lfloor\frac{m}{i}\rfloor+i^2\times\lfloor\frac{n}{i}\rfloor\times\lfloor\frac{m}{i}\rfloor)\\ &=(n^2-\sum_{i=1}^ni\times\lfloor\frac{n}{i}\rfloor)\times(m^2-\sum_{i=1}^mi\times\lfloor\frac{m}{i}\rfloor)-nm\times \min(n,m)+\sum_{i=1}^{\min(n,m)}mi\times\lfloor\frac{n}{i}\rfloor+\sum_{i=1}^{\min(n,m)} ni\times\lfloor\frac{m}{i}\rfloor -\sum_{i=1}^{\min(n,m)} i^2\times\lfloor\frac{n}{i}\rfloor\times\lfloor\frac{m}{i}\rfloor \end{aligned} $$

最后这个 $i^2\times\lfloor\frac{n}{i}\rfloor\times\lfloor\frac{m}{i}\rfloor$ 用数论分块的时候不太一样。首先我们需要保证块内的 $\lfloor\frac{n}{i}\rfloor\times\lfloor\frac{m}{i}\rfloor$ 相同，将右端点改为 $\min(\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor,\lfloor \frac{m}{\lfloor \frac{m}{i} \rfloor} \rfloor)$，这叫做二维数论分块。然后用到结论 $\sum_{i=1}^{n} i^2=\frac{n(n+1)(2n+1)}{6}$。不了解这个结论可以翻到下文数列求和结论 1。

:::info[代码]

long long n, m;
modint pre(modint n) {return n * (n + 1) * (n * 2 + 1) / modint(6);}
modint k1() {  // 这里没法套板子，自己写一个
	modint res = 0;
	for (long long l = 1, r = 0; l <= min(n, m); l = r + 1) {
		r = min(n / (n / l), m / (m / l));
		res += modint(n / l) * modint(m / l) * (pre(r) - pre(l - 1));
	}
	return res;
}

void _main() {
	cin >> n >> m; long long k = min(n, m);
	modint n0 = n, m0 = m;
	modint n1 = n0 * n0 - sqrt_decomposition(n, n,
		[](modint x, modint y) {return (x - y) * (x + y + 1) / 2;}, 
		[](long long x) {return x;} 
	);
	modint m1 = m0 * m0 - sqrt_decomposition(m, m,
		[](modint x, modint y) {return (x - y) * (x + y + 1) / 2;}, 
		[](long long x) {return x;}
	);
	modint n2 = sqrt_decomposition(k, n, 
		[](modint x, modint y) {return (x - y) * (x + y + 1) / 2;}, 
		[&](long long x) {return m0 * x;}
	);
	modint m2 = sqrt_decomposition(k, m, 
		[](modint x, modint y) {return (x - y) * (x + y + 1) / 2;}, 
		[&](long long x) {return n0 * x;}
	);
	cout << n1 * m1 - n0 * m0 * k + n2 + m2 - k1();
}

:::

加法 & 乘法原理

• 加法原理：有 $n$ 类方法，$a_i$ 为第 $i$ 类中方法的数目，则总方法数为 $\sum a_i$。
• 乘法原理：有 $n$ 个步骤，$a_i$ 为第 $i$ 步中方法的数目，则总方法数为 $\prod a_i$。

这两者的区别是：加法分类，乘法分步。

加法原理有一个推论，即减法原理，就是求满足某种约束的方案数可以用总方案数减去不满足约束的方案数。这是最简单的容斥，是“正难则反”的体现。

数列

在应用加法 & 乘法原理推公式的时候，常会用到数列求和相关知识，故在此补充。

等差数列

等差数列是指满足递推式 $a_i-a_{i-1}=d$ 的数列，其中 $d$ 为常数，称作公差。由递推公式逐级写出：

$$a_2-a_1=d\\ a_3-a_2=d\\ \cdots\\ a_{i}-a_{i-1}=d$$

然后两边相加，得

$$a_i=a_1+(i-1)d$$

此为等差数列通项公式。移项可得公差计算方法

$$d=\dfrac{a_i-a_1}{i-1}$$

等差数列求和是 OI 数学题常用方法。下面我们对其作推导。设

$$S=a_1+a_2+\cdots+a_n$$

将其复制一份倒序相加

$$S=a_n+\cdots+a_2+a_1\\ 2S=(a_1+a_n)+(a_2+a_{n-1})+\cdots+(a_n+a_1)=n(a_1+a_n) $$

因而

$$S=\dfrac{a_1+a_n}{2}=na_1+\dfrac{dn(n-1)}{2}$$

等比数列

等差数列是指满足递推式 $\dfrac{a_i}{a_{i-1}}=q$ 的数列，其中 $q$ 为常数，称作公比。类似等差数列的方法可得其递推公式

$$a_i=a_1 \times q^{i-1}$$

仍然来推求和公式。设

$$S=a_1+qa_1+q^2a_1 + \cdots + q^na_1$$

采用错位相减法

$$qS=qa_1+q^2a_1+q^3a_1+\cdots+q^{n+1}a_1\\ qS-S=q^{n+1}a_1-a_1 $$

因此

$$S=\dfrac{(q^{n+1}-1)a_1}{q-1}$$

分治求和法

如果等比数列在模意义下求和，就需要求 $q-1$ 的逆元，而若 $q-1$ 无逆元，则无法套公式。这里介绍一种类似快速幂的分治求和方法，复杂度 $O(\log^2 n)$。

记 $sum(k,n)=1+k+k^2+\cdots+k^{n-1}$。若 $n$ 为偶数，将 $sum(k,n)$ 分为 $1+k+k^2+\cdots+k^{n/2-1}$ 与 $k^{n/2}+\cdots+k^{n-2}+k^{n-1}$ 两部分，则

$$\begin{aligned} sum(k,n)&=1+k+k^2+\cdots+k^n \\ &= 1+k+k^2+\cdots+k^{n/2-1}+k^{n/2}+\cdots+k^{n-2}+k^{n-1} \\ &= 1+k+k^2+\cdots+k^{n/2-1} + k^{n/2}(1+k+k^2+\cdots+k^{n/2-1}) \\ &= (k^{n/2}+1) (1+k+k^2+\cdots+k^{n/2-1}) \\ &= (k^{n/2}+1) \times sum(k,n/2) \end{aligned} $$

而若 $n$ 为奇数，则 $n-1$ 为偶数，$sum(k,n)=sum(k,n-1) + k^{n-1}$。递归出口 $sum(k,1)=1$。

int sum(int k, int n) {
	if (n == 1) return 1;
	if (n & 1) return (sum(k, n - 1) + mpow(k, n - 1)) % p;
	return sum(k, n >> 1) * (mpow(k, n >> 1) + 1) % p;
}

自己造的板子：U588919。

幂数列求和

这里再补充一些幂数列求和的结论。幂数列是形如 $a_i=i^k$ 的数列，$k$ 为正整数。

结论 1：

$$\sum_{i=1}^{n} i = 1+ 2+3+\cdots+n=\dfrac{n(n+1)}{2} $$

等差数列求和的最简单情况，相当常用。$\dfrac{n(n+1)}{2}$ 这个东西叫做三角形数。

结论 2：

$$\sum_{i=1}^{n}i^2 = 1^2+2^2+3^2+\cdots+n^2=\dfrac{n(n+1)(2n+1)}{6} $$

:::success[证明]

用数学归纳法证。显然 $n=1$ 时是成立的。考虑 $n=k$ 时等式成立，只需证 $n=k+1$ 时等式也成立，即

$$1^2+2^2+3^2+\cdots+k^2+(k+1)^2 =\dfrac{k(k+1)(2k+1)}{6}+\dfrac{6(k+1)^2}{6} =\dfrac{(k+1)(k+3)(2k+3)}{6} $$

因此结论正确。

:::

平方数列求和的这个结果 $\dfrac{n(n+1)(2n+1)}{6}$ 又叫做四角锥数。

结论 3：

$$\sum_{i=1}^{n} i^3=1^3+2^3+3^3+\cdots+n^3=(1+2+3+\cdots+n)^2=[\dfrac{n(n+1)}{2}]^2 $$

更高次幂的求和一般不常用。

容斥原理

容斥原理是加法 & 减法原理的推广。

用一个例题引入：假设班里有 $a$ 个学生喜欢语文，$b$ 个学生喜欢数学，$c$ 个数学喜欢英语，则 班里至少喜欢一门学科的有多少个学生？

显然你不能简单地用 $a+b+c$ 计算，因为可以有学生同时喜欢两门甚至三门学科。我们使用集合论语言，设喜欢三门学科的学生集合为 $A,B,C$，则所求为 $|A \cup B \cup C|$。因为 $|A|+|B|+|C|=a+b+c$ 这样会把同时喜欢两个学科的人算重，需要减去 $|A \cap B|+|A \cap C|+ |B \cap C|$。然而这样又会把同时喜欢三个学科的人减去，所以又要加上 $|A \cap B \cap C|$。于是答案为

$$|A \cup B \cup C|=|A|+|B|+|C|-|A \cap B|-|A \cap C|-|B\cap C|+|A \cup B \cup C| $$

这就是三元容斥。它有多元的扩展形式，请读者自行思考。

用到容斥的地方其实很多，减法原理就是最简单的容斥，高维前缀和也有容斥做法，可持久化线段树所使用的 $[l,r]=[1,r]-[1,l-1]$ 也可以用容斥解释。

例题

P3197 [HNOI2008] 越狱

由减法原理，可以用总数目减去不会越狱的数目。

本题中，$n$ 个人都有 $m$ 种选择，由乘法原理可得总数目为 $m^n$。接着我们考虑合法方案，第一个位置能放 $m$ 个，而第二个位置在第一位没有选的 $m-1$ 个中选一个，由此递推，可得方案数为 $m(m-1)^{n-1}$。所以所求为 $m^n-m(m-1)^{n-1}$，并且要写个快速幂。

:::info[代码]

const long long mod = 100003;
long long n, m;

long long power(long long a, long long b) {
	long long res = 1;
	for (a %= mod; b; b >>= 1) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}

void _main() {
	cin >> m >> n;
	cout << ((power(m, n) - m * power(m - 1, n - 1)) % mod + mod) % mod;
}

:::

CF1207D Number Of Permutations

考察好序列的性质，发现不太好计数，于是我们用容斥把它拆开，所求变为：总方案数 $-$ 第一维 $a_i$ 有序的方案数 $-$ 第二维 $b_i$ 有序的方案数 $+$ 两维 $a_i,b_i$ 同时有序的方案数。

显然总方案数是 $n!$。对于单维有序的情况，$a_i,b_i$ 同理，这里只讨论 $a_i$。先完成排序后每一块相同的数可以任意交换，于是我们开个桶来计数，由乘法原理可知答案是 $\prod_{i=1}^{n} cnt_i!$。两维同时有序，和上述类似，我们用桶 $p_{i,j}$ 记录数对 $(i,j)$ 的出现次数，所求为 $\prod_{i=1}^{n} p_{a_i,b_i}$。于是我们预处理阶乘即可。

但是要注意两维同时有序可能无解，需要排个序特判一波。

以及：CF 有 hack 机制能用 unordered_map 吗？

:::info[代码]

const int N = 3e5 + 5;
using p32 = pair<int, int>;

mint fac[N];
int n, a, b;
p32 h[N];
map<int, int> cnt1, cnt2;
map<p32, int> p;

void _main() {
	cin >> n;
	fac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i;
	for (int i = 1; i <= n; i++) {
		cin >> a >> b, h[i] = make_pair(a, b);
		cnt1[a]++, cnt2[b]++, p[h[i]]++;
	}
	sort(h + 1, h + n + 1);
	mint c0 = fac[n], c1 = 1, c2 = 1, c12 = 1;
	for (int i = 2; i <= n; i++) {
		if (h[i].second < h[i - 1].second) c12 = 0;
	}
	for (const auto& i : cnt1) c1 *= fac[i.second];
	for (const auto& i : cnt2) c2 *= fac[i.second];
	for (const auto& i : p) c12 *= fac[i.second];
	cout << c0 - c1 - c2 + c12;
} 

:::

P1447 [NOI2010] 能量采集

组合数学的原理也可以解决数论问题。在前面的欧拉函数部分，我们知道这样的问题答案是

$$\sum_{i=1}^{n} \sum_{j=1}^{m} (2\times\gcd(i, j)-1)=2\sum_{i=1}^{n} \sum_{j=1}^{m} \gcd(i,j)-nm $$

可以发现 $\gcd(i,j)$ 的值只有 $n$ 种，不妨考虑 $gcd(i,j)=k$ 的数目，设其数目为 $f(k)$。我们可以考虑求以 $k$ 为公约数的数对数目，再减去以 $k$ 的倍数为公约数的数对数目。进一步推导，以 $k$ 的倍数为公约数的数对个数等于所有以 $k$ 的倍数为最大公约数的数对个数之和。于是有

$$f(k)=\lfloor \dfrac{n}{k} \rfloor \times\lfloor \dfrac{m}{k} \rfloor -\sum_{i=2}^{ik \le \min(n,m)} f(ik) $$

我们发现 $2k > \min(n,m)$ 时 $f(k)=\lfloor \dfrac{n}{k} \rfloor \times\lfloor \dfrac{m}{k} \rfloor$，于是倒着算就行了，是调和型枚举，复杂度 $O(n \log n)$。于是 GCD SUM 问题就多了一种容斥做法。

:::info[代码]

const int N = 1e5 + 5;
long long f[N];
int n, m;

void _main() {
	cin >> n >> m;
	for (int k = n; k >= 1; k--) {
		f[k] = 1LL * (n / k) * (m / k);
		for (int i = 2; i * k <= min(n, m); i++) f[k] -= f[i * k];
	}
	long long res = 0;
	for (int i = 1; i <= n; i++) res += f[i] * i;
	cout << res * 2 - 1LL * n * m;
}

:::

AT_abc162_e [ABC162E] Sum of gcd of Tuples (Hard)

笔者数论训练赛の T5。和上面题的套路一样，我们发现，$\gcd a_i=k$ 时当且仅当 $a_1,a_2, \cdots,a_n$ 均为 $k$ 的倍数，且这个倍数是互质的。考虑容斥 + DP，令 $dp_x$ 表示 $[1,x]$ 内选出 $n$ 个互质数的方法数目。考虑用减法原理，总数目减去不互质的方案，枚举公约数 $i$，则根据约数性质可得

$$dp_x=x^n-\sum_{i=2}^{x} dp_{\lfloor \frac{x}{i} \rfloor} $$

赛时写的记搜。可以发现这个东西也是容斥思想。

:::info[代码]

int n, k;
mint dp[N];
mint solve(int x) {
	if (dp[x] != 0) return dp[x]; 
	if (x == 1) return dp[x] = 1;
	mint res = mint(x).pow(n);
	for (int i = 2; i <= x; i++) {
		res -= solve(x / i); 
	} return dp[x] = res;
}

void _main() {
	cin >> n >> k;
	mint res = 0;
	for (int i = 1; i <= k; i++) res += solve(k / i) * i;
	cout << res;
} 

:::

AT_abc366_d [ABC366D] Cuboid Sum Query

三维前缀和板子题，容斥原理的另一种应用。我们先来推三维前缀和怎么算。设 $pre_{i,j,k}$ 表示以 $(i,j,k)$ 为右下角的立方体数字之和，则它显然由 $a_{i,j,k}$ 贡献。同时考虑去掉一行 / 一列 / 一柱，加上 $pre_{i-1,j,k}+pre_{i,j-1,k}+pre_{i,j,k-1}$。这样我们会把同时退掉两维的前缀和算重，于是减去 $pre_{i-1,j-1,k}+pre_{i-1,j,k-1}+pre_{i,j-1,k-1}$。这样又把退掉三维的前缀和减多了，所以加上 $pre_{i-1,j-1,k-1}$。总的转移为

$$。pre_{i,j,k}=a_{i,j,k}+pre_{i-1,j,k}+pre_{i,j-1,k}+pre_{i,j,k-1}-pre_{i-1,j-1,k}-pre_{i-1,j,k-1}-pre_{i,j-1,k-1}+pre_{i-1,j-1,k-1} $$

接着我们考虑单次询问以 $(x_1,y_1,z_1)$ 为左上角，$(x_2,y_2,z_2)$ 为右下角的立方体点权之和。同理可得答案为

$$pre_{x_2,y_2,z_2}-pre_{x_1-1,y_2,z_2}-pre_{x_2,y_1-1,z_2}-pre_{x_2,y_2,z_1-1}+pre_{x_1-1,y_1-1,z_2}+pre_{x_1-1,y_2,z_1-1}+pre_{x_2,y_1-1,z_1-1}-pre_{x_1-1,y_1-1,z_1-1} $$

于是我们在预处理 $O(n^3)$，查询 $O(1)$ 下解决了该问题。

:::info[代码]

const int N = 105;
int n, q, a[N][N][N], pre[N][N][N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			for (int k = 1; k <= n; k++) cin >> a[i][j][k];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			for (int k = 1; k <= n; k++) {
				pre[i][j][k] = a[i][j][k]
				+ pre[i][j][k - 1] + pre[i][j - 1][k] + pre[i - 1][j][k]
				- pre[i][j - 1][k - 1] - pre[i - 1][j][k - 1] - pre[i - 1][j - 1][k]
				+ pre[i - 1][j - 1][k - 1];
			}
		}
	}
	cin >> q;
	while (q--) {
		int x1, x2, y1, y2, z1, z2;
		cin >> x1 >> x2 >> y1 >> y2 >> z1 >> z2;
		cout << (pre[x2][y2][z2] 
		- pre[x1 - 1][y2][z2] - pre[x2][y1 - 1][z2] - pre[x2][y2][z1 - 1]
		+ pre[x1 - 1][y1 - 1][z2] + pre[x1 - 1][y2][z1 - 1] + pre[x2][y1 - 1][z1 - 1]
		- pre[x1 - 1][y1 - 1][z1 - 1]) << '\n';
	}
}

:::

P6651 「SWTR-5」Chain

一步一步考虑，先想无修改怎么做，我们在拓扑序上做 DP，由加法原理

$$f_{i} \gets f_{i}+f_j$$

进一步地，由于 $n\le 2\times 10^3$，我们可以利用拓扑排序，在 $O(n^2)$ 时间内预处理从 $u$ 到 $v$ 的链数，则

$$dp_{k,v} \gets dp_{k,v}+dp_{k,u}$$

类似 Floyd 那样，对于有向边 $(u,v)$，枚举中继点 $k \in [1,n]$，由加法原理合并。记入度为 $ideg_i$，出度为 $odeg_i$，则总链数

$$tot=\sum_{ideg_i=0} \sum_{odeg_j=0} dp_{i,j}$$

因为一条链的起终点一定满足上述条件。接着我们考虑 $k=1$ 的做法，套路地，记 $f_i$ 为链起点到点 $i$ 的方案数，然后建反图，记 $g_i$ 是反图上的 $f_i$，发现 $g_i$ 等价于原图中点 $i$ 到链终点的方案数。由 $dp_{i,j}$ 的定义易得转移：

$$f_i = \sum_{ideg_j=0} dp_{j,i}\\ g_i = \sum_{odeg_j=0} dp_{i,j} $$

那么 $k=1$ 的情况就可以用 $tot-f_ig_i$ 回答。接着我们想 $k=2$，不妨设两点 $u,v$ 中 $u$ 的拓扑序小于 $v$，分类讨论：

• 若 $u,v$ 不在同一条链上，直接用 $tot-f_ug_u-f_vg_v$ 回答；
• 若 $u,v$ 可以在同一条链上，那么 $u$ 到终端的路径包含了 $v$。考虑容斥把重复的加回来，这里的重复是 $f_ug_v dp_{u,v}$，答案为 $tot-f_ug_u-f_vg_v+f_ug_v dp_{u,v}=tot-f_ug_u-g_v(f_v-f_udp_{u,v})$。

接着我们扩展到 $k \le 15$。我们先按拓扑序排序，对于每个点处理要容斥掉的数 $h_i$，则

$$h_i=f_i-\sum h_j dp_{j,i}$$

其中 $j$ 的拓扑序在 $i$ 之前。于是答案为

$$tot-\sum h_ig_i$$

至此，我们在预处理 $O(n^2+m)$，单次查询 $O(k^2)$ 的复杂度下解决了此问题。

:::info[代码]

const int N = 2e3 + 5, M = 2e4 + 5;

int tot = 0, head[N];
struct Edge {
	int next, to;
} edge[M];
inline void add_edge(int u, int v) {
	edge[++tot].next = head[u], edge[tot].to = v, head[u] = tot;
}
int n, m, u, v, q, len, ideg[N], odeg[N];

int cnt, bfn[N];
mint dp[N][N], f[N], g[N], h[20];
void topo() {
	queue<int> q;
	for (int i = 1; i <= n; i++) {
		if (ideg[i] == 0) q.emplace(i);
		dp[i][i] = 1;
	}
	while (!q.empty()) {
		int u = q.front(); q.pop();
		bfn[u] = ++cnt;
		for (int j = head[u]; j != 0; j = edge[j].next) {
			int v = edge[j].to;
			for (int k = 1; k <= n; k++) dp[k][v] += dp[k][u];
			if (--ideg[v] == 0) q.emplace(v);
		}
	}
}

vector<int> st, ed;
void _main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		cin >> u >> v;
		add_edge(u, v);
		odeg[u]++, ideg[v]++;
	} 
	for (int i = 1; i <= n; i++) {
		if (ideg[i] == 0) st.emplace_back(i);
		if (odeg[i] == 0) ed.emplace_back(i);
	} topo();
	mint tot = 0;
	for (int i : st) {
		for (int j : ed) tot += dp[i][j];
	}
	for (int i = 1; i <= n; i++) {
		for (int j : st) f[i] += dp[j][i];
		for (int j : ed) g[i] += dp[i][j];
	}
	for (cin >> q; q--; ) {
		fill(h, h + len, 0);
		cin >> len;
		vector<int> c;
		for (int i = 0; i < len; i++) cin >> u, c.emplace_back(u);
		sort(c.begin(), c.end(), [](int x, int y) -> bool {
			return bfn[x] < bfn[y];
		});
		for (int i = 0; i < len; i++) {
			h[i] = f[c[i]];
			for (int j = 0; j < i; j++) h[i] -= dp[c[j]][c[i]] * h[j];
		}
		mint res = 0;
		for (int i = 0; i < len; i++) res += h[i] * g[c[i]];
		cout << tot - res << '\n';
	}
}

:::

排列组合

排列

从 $n$ 个不同元素中取 $m$ 个元素排成有序的一列，方案数用 $A_{n}^{m}$ 表示。

我们这样计算：第一个数有 $n$ 种选法，第二个数有 $n-1$ 种选法……第 $m$ 个数有 $n-m+1$ 种选法，由乘法原理得

$$A_{n}^{m}=n(n-1)(n-2) \cdots (n-m+1)=\prod_{i=n-m+1}^{n} i=\dfrac{n!}{(n-m)!} $$

规定 $m>n$ 时 $A_{n}^{m}=0$。

而如果 $m=n$，也就是所有元素都参与排列，此时称为全排列。全排列的计算

$$A_{n}^{n}=n!$$

全排列的枚举

在 C++ 标准库中提供了 next_permutation 函数，可以这样使用：

// a为要枚举排列的数组，n为长度
sort(a + 1, a + n + 1);
do {
  ...
} while (next_permutation(a + 1, a + n + 1));

时间复杂度为 $O(n!)$。

有重复元素的排列问题

顾名思义就是元素有重，此时需要除去重复的排列。

考虑一组有 $m$ 个的重复元素，其造成重复的个数就是它在排列中的次序交换，也就是 $m!$ 种情况，所以总排列数

$$\dfrac{n!}{m_1!m_2!m_3! \cdots}$$

其中 $n$ 为总元素个数，$m$ 为各元素出现次数。

圆排列

从 $n$ 个不同元素中取 $m$ 个元素排成有序的一圈，方案数用 $Q_{n}^{m}$ 表示。考虑断环为链，共有 $m$ 个断点，故

$$Q_{n}^{m}=\dfrac{A_{n}^{m}}{m}=\dfrac{n!}{m(n-m)!} $$

康托展开

康托展开解决的是求排列字典序的问题。先给出公式：

$$1+\sum_{i=1}^{n} rk_i \times (n-i)!$$

其中 $rk_i$ 表示 $[i,n]$ 中有多少个数小于 $a_i$，即 $a_i$ 的后缀排名。理解一下这个公式，字典序就是比当前排列小的排列数目，贪心地枚举 $i$，使得第 $i$ 为小于 $a_i$，而后置位与字典序无关。那么我们就需要把 $i$ 后面小于 $a_i$ 的数换到前面，且根据全排列的原理有 $(n-i)!$ 种方案。

康托展开还有一种进制意义，可以看 yummy 大佬的 blog。

组合

从 $n$ 个不同元素中取 $m$ 个元素组成无序的一个集合，方案数用 $C_{n}^{m}$ 表示。

考虑先作排列，由于集合无序，需要除去重复的组合，也就是 $m$ 的全排列，逆用乘法原理：

$$C_{n}^{m}=\dfrac{A_{n}^{m}}{m!}=\dfrac{n!}{m!(n-m)!} $$

规定 $m>n$ 时 $C_{n}^{m}=0$。

组合的枚举

代码如下：

int n, m, cur[N];
void dfs(int x) {
	if (x > m) return ..., void();  // 这里cur就是一个组合，进行处理
	for (int i = cur[x - 1] + 1; i <= n; i++) cur[x] = i, dfs(x + 1);
}

dfs(1);

它用于枚举 $1$ 到 $n$ 所有自然数选 $m$ 个的组合。如果套上 next_permutation，还能实现排列的枚举。

二项式定理

$$(a+b)^n=\sum_{i=0}^{n} C_{n}^{i} a^{n-i} b^{i}$$

这个定理表明，二项式 $(a+b)^n$ 展开项的系数与组合数有直接关系。

我们知道杨辉三角：

其每一个位置的数字通过左上 + 右上确定，每一行所对应的就是二项式展开的系数。

组合数的性质

1. 对称性：

$$C_{n}^{m} = C_{n}^{n-m}$$

代数推导易证，组合意义就是把选出的集合取补集。

2. 递推式：

$$C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$$

代数推导略去，组合意义类似 dp 的思想可以证明。这个式子实际上就是杨辉三角的递推式。

3. 二项式定理的特殊情况 1：

$$2^n=\sum_{i=0}^{n} C_n^i$$

也就是杨辉三角每一行的和。

4. 斐波那契数列：

$$fib_{n+1}=\sum_{i=0}^{n} C_{n-i}^i$$

把杨辉三角每条斜 $30 \degree$ 角的线取出来相加可以发现。

5. 范德蒙恒等式：

$$C_{m+n}^{k}=\sum_{i=0}^{k} C_m^i C_n^{k-i}$$

:::success[证明]

假设有两堆物品，每堆分别有 $m,n$ 个物品，总共取 $k$ 个，则方案数可分解为：从第一堆取 $i$ 个物品，第二堆取 $k-i$ 个物品，且两种选择独立，故由乘法得到贡献。最后方案即为求和。

:::

6. 二项式定理的特殊情况 2：

$$\sum_{i=0}^{n} (-1)^i C_n^i = 0$$

特殊情况是 $n=0$ 时上式的值为 $1$。

计算组合数

定义法

• 优点：写起来简单，不用预处理。
• 缺点：查询复杂度 $O(m)$。

根据定义直接计算，注意先乘后除。

:::info[实现]

inline long long C(int n, int m) {
	if (m > n) return 0;
	long long res = 1;
	for (int i = 1; i <= m; i++) {
		res = res * (n - i + 1) % mod * power(i, mod - 2) % mod;
	}
	return res;
}

:::

递推法

• 优点：任意模数，写起来简单，查询 $O(1)$。
• 缺点：预处理时空复杂度均为 $O(n^2)$。

即利用组合数性质 2 预处理杨辉三角。

:::info[实现]

for (int i = 0; i < N; i++) c[i][0] = 1, c[i][i] = 1;
for (int i = 0; i < N; i++) {
  for (int j = 1; j < i; j++) c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
}

:::

逆元法

• 优点：预处理 $O(n)$，查询 $O(1)$。
• 缺点：只能在模数为质数时使用。

通过预处理阶乘和阶乘的逆元，直接用定义式计算组合数。

:::info[实现]

inline long long power(long long a, long long b) {
	long long res = 1;
	for (a %= mod; b; b >>= 1) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}

long long fac[N], ifac[N];
inline void pre() {
	fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
	for (int i = 2; i < N; i++) fac[i] = fac[i - 1] * i % mod, ifac[i] = power(fac[i], mod - 2);
}

inline long long C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] % mod * ifac[n - m] % mod; 
}

:::

Lucas 定理法

• 优点：预处理 $O(p)$，查询 $O(\log n)$，适用于模数小而 $n,m$ 很大的情况。
• 缺点：码量稍大，只能处理 $p$ 为质数的情况。

Lucas 定理如下：

$$C_n^m \equiv C_{n \bmod p}^{m \bmod p} C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor} \pmod p $$

其中 $p$ 是质数。利用这个式子，先用逆元法预处理所有 $p$ 以内的组合数，查询时递归计算即可。

:::info[实现]

inline long long power(long long a, long long b) {
	long long res = 1;
	for (a %= mod; b; b >>= 1) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}

long long fac[N], ifac[N];
inline void pre() {
	fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
	for (int i = 2; i < N; i++) fac[i] = fac[i - 1] * i % mod, ifac[i] = power(fac[i], mod - 2);
}

inline long long C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] % mod * ifac[n - m] % mod; 
}
long long lucas(long long n, long long m) {
	if (m == 0) return 1;
	if (n < mod && m < mod) return C(n, m);
	return lucas(n / mod, m / mod) * C(n % mod, m % mod) % mod;
}

:::

P3807 【模板】卢卡斯定理/Lucas 定理。

Lucas 定理可以实现快速求组合数前缀和，可以看例题中的 P4345 [SHOI2015] 超能粒子炮·改。

exLucas 法

• 优点：任意模数，预处理约为 $O(p \log p)$，查询 $O(\log p)$，同样适用于模数小而 $n,m$ 很大的情况。
• 缺点：码量很大。

exLucas 跟 Lucas 没有半毛钱关系。

将模数 $p$ 质因数分解为 $p=p_1^{a_1} p_2^{a_2} \cdots$，然后计算 $C_n^m \bmod p^a$，最后再把答案用 exCRT 合并（可见下方数论部分）。

现在的重点是算 $C_n^m \bmod p^a$，由定义式得所求即为 $\dfrac{n!}{m!(n-m)!} \bmod p^a$，只要求出阶乘及逆元即可。先将阶乘中 $p$ 的倍数算掉，即 $\lfloor \dfrac{n}{p}\rfloor!$，而剩余项存在循环节，可以一起计算，凑不进循环节的单独算。

For example：

$$\begin{aligned} 20!&=1\times 2\times 3\times 4\times 5\times 6\times 7\times 8\times 9\times 10\times 11\times 12\times 13\times 14\times 15\times 16\times 17\times 18\times 19\times 20\\ &=(1\times 2\times 4\times 5\times 7\times 8\times 10\times 11\times 13\times 14\times 16\times 17\times 19\times 20) \times 6! \times 3^6\\ &=(1\times 2 \times 4 \times 5 \times 7 \times 8)^2\times 19 \times 20 \times 6! \times 3^6 \end{aligned} $$

至于阶乘逆元，用 exGCD 求得即可。

:::info[实现]

inline long long power(long long a, long long b, long long p) {
	long long res = 1;
	for (a %= p; b; b >>= 1) {
		if (b & 1) res = res * a % p;
		a = a * a % p;
	}
	return res;
}

void exgcd(long long a, long long b, long long& x, long long& y) {
	if (b == 0) return x = 1, y = 0, void();
	exgcd(b, a % b, x, y);
	int t = x;
	x = y, y = t - a / b * y;
}
inline long long inverse(long long x, long long p) {
	long long a, b;
	exgcd(x, p, a, b);
	return (a % p + p) % p;
}

inline long long calc(long long n, long long x, long long p) {
	if (n == 0) return 1;
	long long s = 1;
	for (long long i = 1; i <= p; i++) {
		if (i % x) s = s * i % p;
	}
	s = power(s, n / p, p);
	for (long long i = n / p * p + 1; i <= n; i++) {
		if (i % x) s = i % p * s % p;
	}
	return s * calc(n / x, x, p) % p;
}

inline long long multilucas(long long m, long long n, long long x, long long p) {
	int cnt = 0;
	for (long long i = m; i; i /= x) cnt += i / x;
	for (long long i = n; i; i /= x) cnt -= i / x;
	for (long long i = m - n; i; i /= x) cnt -= i / x;
	return power(x, cnt, p) % p * calc(m, x, p) % p * inverse(calc(n, x, p), p) % p
		   * inverse(calc(m - n, x, p), p) % p;
}

long long x[20];
inline int crt(int n, long long* a, long long* m) {
	long long mod = 1, res = 0;
	for (int i = 1; i <= n; i++) mod *= m[i];
	for (int i = 1; i <= n; i++) {
		x[i] = mod / m[i];
		long long x0 = -1, y0 = -1;
		exgcd(x[i], m[i], x0, y0);
		res += a[i] * x[i] * (x0 >= 0 ? x0 : x0 + m[i]);
	}
	return res % mod;
}

inline long long exlucas(long long m, long long n, long long p) {
	int len = 0;
	long long p0[20], a0[20];
	for (long long i = 2; i * i <= p; i++) {
		if (p % i) continue;
		p0[++len] = 1;
		while (p % i == 0) p0[len] *= i, p /= i;
		a0[len] = multilucas(m, n, i, p0[len]);
	}
	if (p > 1) p0[++len] = p, a0[len] = multilucas(m, n, p, p);
	return crt(len, a0, p0);
}

:::

P4720 【模板】扩展卢卡斯定理/exLucas。

经典模型

这里介绍排列组合题里常用的转化思想，每种模型给出一些例题。

捆绑法

Q: 有 $n+m$ 个不同元素要进行排列，其中 $m$ 个元素必须连续，求方案数。

A: 将 $m$ 个元素捆绑在一起，内部排列方案为 $m!$ 种，这 $m$ 个元素的整体视为一个元素，则外部排列方案为 $(n+1)!$ 种，由乘法原理得方案数为 $(n+1)!m!$。

插空法

Q: 有 $n+m$ 个不同元素要进行排列，其中 $m$ 个元素必须两两不相邻，求方案数。

A: 先将 $n$ 个元素全排列，再求 $n+1$ 个空隙而插入 $m$ 块板子的方案数为 $A_{n+1}^{m}$，所以方案数为 $n! A_{n+1}^{m}$。

插板法

Q1: 现有 $n$ 个相同元素，分为 $k$ 组，每组至少有一个元素，求方案数。
（可以抽象为：求方程 $x_1+x_2+\cdots+x_k=n$ 的正整数解数目）

A1: 不考虑分组，而是考虑间断点，将 $k-1$ 块板子插入到 $n-1$ 个空里，则答案为 $C_{n-1}^{k-1}$。

Q2: 现有 $n$ 个相同元素，分为 $k$ 组，每组可以为空，求方案数。
（可以抽象为：求方程 $x_1+x_2+\cdots+x_k=n$ 的非负整数解数目）

A2: 先借 $k$ 个元素过来放到每组里，由 Q1 可得方案数为 $C_{n+k-1}^{k-1}=C_{n+k-1}^{n}$，再把 $k$ 个元素拿走，方案数不变。

Q3: 现有 $n$ 个相同元素，分为 $k$ 组，第 $i$ 组的元素数目不小于 $a_i$，求方案数。
（可以抽象为：求方程 $x_1+x_2+\cdots+x_k=n$ 的解数目，其中 $x_i \ge a_i$）

A3: 先借 $\sum a_i$ 个元素过来，令 $x_i'=x_i-a_i$，可知 $\sum x_i'=n-\sum a_i$，由 Q2 得答案为 $C_{n-\sum a_i+k-1}^{n-\sum a_i}$。

二项式反演

如果某些计数问题的限制是“某些物品恰好若干个”，就可以考虑使用二项式反演。

原理

设 $f_n$ 表示恰好使用 $n$ 个不同元素形成特定结构的方案数，$g_n$ 表示从这 $n$ 个不同元素中选出若干个元素形成特定结构的方案数。

已知 $f_n$ 求 $g_n$ 是简单的，枚举选出多少个元素有

$$g_n=\sum_{i=0}^{n} C_n^i f_i$$

反着做却是困难的，这个过程就叫二项式反演。有公式：

$$f_n=\sum_{i=0}^{n} C_n^i (-1)^{n-i}g_i$$

二项式反演的作用就是把“恰好”转化为“钦定”。

:::success[证明]

我们先给出一个引理

$$C_n^r C_r^k=C^k_n C^{r-k}_{n-k}$$

组合意义和代数推导都易证。

把上述式子展开：

$$\begin{aligned} f_n&=\sum_{i=0}^{n} C_n^i (-1)^{n-i} [\sum_{j=0}^{i} C_i^j f_j]\\ &=\sum_{i=0}^{n} \sum_{j=0}^{i} C_n^i C_i^j (-1)^{n-i} f_j \\ &= \sum_{j=0}^{n} \sum_{i=j}^{n} C_n^i C_i^j (-1)^{n-i} f_j \\ &= \sum_{j=0}^{n} [f_j \times \sum_{i=j}^{n} C_n^i C_i^j (-1)^{n-i} ] \end{aligned} $$

根据引理可得

$$\begin{aligned} f_n&=\sum_{j=0}^{n} [f_j \times \sum_{i=j}^{n} C_n^j C_{n-j}^{i-j} (-1)^{n-i} ]\\ &=\sum_{j=0}^{n} [C_n^j f_j \times \sum_{i=j}^{n}C_{n-j}^{i-j} (-1)^{n-i} ]\\ \end{aligned} $$

作换元，令 $k=i-j$，则 $i=k+j$，即有

$$\begin{aligned} f_n&=\sum_{j=0}^{n} [C_n^j f_j \times \sum_{k=0}^{n-j}C_{n-j}^{k} (-1)^{n-j-k} ]\\ &=\sum_{j=0}^{n} [C_n^j f_j \times \sum_{k=0}^{n-j}C_{n-j}^{k} (-1)^{n-j-k}1^k ] \end{aligned} $$

由组合数性质 6 可得当且仅当 $n=j$ 时 $\sum_{k=0}^{n-j}C_{n-j}^{k} (-1)^{n-j-k}1^k$ 为 $1$，故：

$$f_n=f_n$$

由此可以证明二项式反演。

:::

例题

排列组合的题一般有两种，一种是看着就是数学题去推公式，还有一种就是给了你某些操作，你考察操作的一些性质并结合分类讨论抽象一个组合数学的模型，然后解决问题。

P2822 [NOIP 2016 提高组] 组合数问题

我们用二维数组 $c_{i,j}$ 表示 $C_i^j$，然后用二维前缀和预处理 $i \in [0,n], j \in [0, \min(i,m)]$ 中有多少 $k \mid c_{i,j}$，每次 $O(1)$ 查询即可。

:::info[代码]

const int N = 2005;
int t, k, n, m, c[N][N], pre[N][N];

void _main() {
	cin >> t >> k;
	c[1][1] = 1;
	for (int i = 0; i < N; i++) c[i][0] = 1;
	for (int i = 2; i < N; i++) {
		for (int j = 1; j <= i; j++) {
			c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % k;
		}
	}
	for (int i = 2; i < N - 1; i++) {
		for (int j = 1; j <= i; j++) {
			pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + (c[i][j] == 0);
		}
		pre[i][i + 1] = pre[i][i];
	}
	while (t--) {
		cin >> n >> m;
		if (m > n) m = n;   // 注意细节
		cout << pre[n][m] << '\n';
	}
}

:::

P3223 [HNOI2012] 排队

高中月考题（

考虑减法原理，用女生不相邻的方案数减去女生不相邻而老师相邻的方案数。

求女生不相邻的方案数，用插空法，如果已经排好了 $2$ 个老师和 $n$ 个男生，则会形成 $n+3$ 个空位，在空位上排列 $m$ 个女生即可。由乘法原理，方案数是 $A_{n+2}^{n+2} A_{n+3}^m$。

再考虑求女生不相邻而老师相邻的方案数。用捆绑法，现将老师视为整体，内部方案数为 $A_2^2$；再用插空法，一个老师的整体与 $n$ 个男生形成 $n+1$ 个空位，同理可得方案数为 $A_{n+1}^{n+1}A_{n+2}^{m}$。

综上所述，答案为

$$A_{n+2}^{n+2} A_{n+3}^m-A_2^2A_{n+1}^{n+1}A_{n+2}^{m} $$

注意要用高精度。

:::info[代码]

int n, m;
BigInteger A(int m, int n) {
	BigInteger res = 1;
	for (int i = n - m + 1; i <= n; i++) res *= i;
	return res;
}

void _main() {
	cin >> n >> m;
 	cout << A(n + 2, n + 2) * A(m, n + 3) - A(2, 2) * A(n + 1, n + 1) * A(m, n + 2);
}

:::

P11250 [GESP202409 八级] 手套配对

首先先从 $n$ 对手套中拿出 $k$ 对，方案数 $C_n^k$。又因为要恰好拿走 $k$ 对手套，说明剩下的 $m-2k$ 只手套中不能同时选走一对，从其中取出 $m$ 对左或右手套，由乘法原理得答案为 $2^{m-2k} \times C_{n-k}^{m-2k}$，最后再用乘法原理合并答案。预处理组合数用杨辉三角即可。

:::info[代码]

const int N = 2005;
int n, m, k;
modint c[N][N];

void _main() {
	cin >> n >> m >> k;
	if (m < 2 * k) return cout << 0 << '\n', void();
	cout << c[n][k] * c[n - k][m - 2 * k] * modint(2).pow(m - 2 * k) << '\n';
} signed main() {
	for (int i = 0; i < N; i++) c[i][0] = 1, c[i][i] = 1;
	for (int i = 0; i < N; i++) {
		for (int j = 1; j < i; j++) c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
	}
	int t = 1; for (cin >> t; t--; ) _main();
}

:::

P5367 【模板】康托展开

康托展开板子题，但你要是直接按公式求是 $O(n^2)$ 的。显然枚举 $i$ 不能删，瓶颈在计算 $rk_i$，使用权值树状数组维护即可。

实现时，可以把树状数组上每个位置都加一，然后出现了这个数再减一，这样 $rk_i$ 转化为树状数组前缀求和。复杂度 $O(n \log n)$。

:::info[代码]

const int N = 1e6 + 5;
int n, a[N];

int tr[N];
void add(int x, int c) {for (; x <= n; x += (x & -x)) tr[x] += c;}
int ask(int x) {
	int res = 0;
	for (; x != 0; x -= (x & -x)) res += tr[x];
	return res;
}

mint fac[N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	fac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i, add(i, 1);
	mint res = 1;  // 初值为1
	for (int i = 1; i <= n; i++) res += fac[n - i] * (ask(a[i]) - 1), add(a[i], -1);
	cout << res;
}

:::

P3014 [USACO11FEB] Cow Line S

这题多了一个给定排名求排列的操作，就是把康托展开的过程反过来。具体可见代码，并且这个逆操作也是可以用权值树状数组 / 权值线段树维护的，但是这题没有必要。具体过程很类似进制转换。

:::info[代码]

int n, q, a[N], ans[N];
long long x, fac[N], w[N];
char opt;

long long tr[N];
void add(int x, long long c) {for (; x <= n; x += (x & -x)) tr[x] += c;}
long long ask(int x) {
	long long res = 0;
	for (; x != 0; x -= (x & -x)) res += tr[x];
	return res;
}
int kth(int k) {
	long long pos = 0, x = 0;
	for (int i = __lg(n); i >= 0; i--) {
		x += (1 << i);
		if (x >= n || pos + tr[x] >= k) x -= (1 << i);
		else pos += tr[x];
	} return x + 1;
}

void _main() {
	cin >> n >> q;
	fac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i;
	while (q--) {
		memset(tr, 0, sizeof(tr));
		cin >> opt;
		if (opt == 'Q') {
			for (int i = 1; i <= n; i++) cin >> a[i], add(i, 1);
			long long res = 1;  
			for (int i = 1; i <= n; i++) res += fac[n - i] * (ask(a[i]) - 1), add(a[i], -1);
			cout << res << '\n';
		} else if (opt == 'P') {
			cin >> x; x--;
			for (int i = 1; i <= n; i++) w[n - i + 1] = x % i, x /= i, add(i, 1);
			for (int i = 1; i <= n; i++) ans[i] = kth(w[i] + 1), add(ans[i], -1);
			for (int i = 1; i <= n; i++) cout << ans[i] << ' ';
			cout << '\n';
		}
	}
}

:::

数据范围更大的逆康托展开模板：UVA11525。

CF1436C Binary Search

考虑二分查找的过程，由于 $n$ 是固定的，则二分查找的路径是唯一的，因此我们可以求出一定小于等于 $x$ 的数的个数，一定大于 $x$ 的数的个数，分别记作 $a,b$。那么在小于等于 $x$ 的 $x-1$ 个数中，就要找 $a-1$ 个数出来排列（因为还有一个数等于 $x$） ，而大于 $x$ 的 $n-x$ 个数中找 $b$ 个来排列，剩下的任意排列，是全排列。

由乘法原理可得答案

$$A_{x-1}^{a-1} A_{n-x}^{b} A_{n-a-b}^{n-a-b}$$

计算排列数也可以用逆元法。

:::info[代码]

const int N = 1005;
int n, x, pos;
mint fac[N], ifac[N];
mint A(int m, int n) {
	if (m > n) return 0;
	return fac[n] * ifac[n - m];
}

void _main() {
	cin >> n >> x >> pos;
	int l = 0, r = n, a = 0, b = 0;
	while (l < r) {
		int mid = (l + r) >> 1;
		if (mid <= pos) l = mid + 1, a++;
		else r = mid, b++;
	} fac[0] = 1, ifac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	cout << A(a - 1, x - 1) * A(b, n - x) * A(n - a - b, n - a - b);
}

:::

P9306 「DTOI-5」进行一个排的重 (Minimum Version)

考虑 $f(a)$ 的计算方法，可以发现就是 $p_i,q_i$ 是否为 $[1,i]$ 的前缀最值。显然，若存在 $i \in [1,n]$ 使得 $p_i=q_i=n$，直接把这个换到前面去，其他的数任意排列都不会产生贡献，因此答案为 $2$ 和 $(n-1)!$。

通过上述讨论，我们发现 $p_i=n$ 和 $q_j=n$ 的位置是关键的。若不存在上述 $i$，手玩一下把 $p_i=n$ 的一项放到前面去，可以构造答案为 $3$。方案如下：第一项贡献为 $2$，而 $q_j$ 必然产生 $1$ 的贡献，如果不产生其他贡献，就必须在 $q_i$ 前放小于它的数。逆用乘法原理，在 $(n-1)!$ 的原方案中除去 $n-q_i$，故答案为 $\dfrac{(n-1)!}{n-q_i}$。把 $q_j$ 放到前面的方案同理，由加法原理合并答案为

$$\dfrac{(n-1)!}{n-q_i}+\dfrac{(n-1)!}{n-p_j}$$

代码分类讨论一下即可。

:::info[代码]

const int N = 5e5 + 5;
int n, p[N], q[N];
mint factorial(int x) {
	mint res = 1;
	for (int i = 2; i <= x; i++) res *= i;
	return res;
}
void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> p[i];
	for (int i = 1; i <= n; i++) cin >> q[i];
	int i = 1, j = 1;
	for (int x = 1; x <= n; x++) {
		if (p[x] == n) i = x;
		if (q[x] == n) j = x;
	}
	if (i == j) cout << "2 " << factorial(n - 1);
	else cout << "3 " << factorial(n - 1) / (n - q[i]) + factorial(n - 1) / (n - p[j]);
} 

:::

CF1696E Placing Jinas

显然是从格子 $(0,0)$ 开始操作，一路递推，故设 $(x,y)$ 的末值为 $f_{x,y}$，则

$$f_{x,y}=f_{x-1,y}+f_{x,y-1}$$

对比杨辉三角的计算方法（组合数性质 2）

$$C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$$

发现两者很像，考虑用组合数表示 $f_{x,y}$。对比两者系数可得

$$f_{x,y}=C_{x+y}^{x}$$

因此答案为

$$\sum_{i=0}^{n} \sum_{j=0}^{a_i-1} f_{i,j}=\sum_{i=0}^{n} \sum_{j=0}^{a_i-1} C^{i}_{i+j} $$

预处理逆元后复杂度为 $O(nV)$，无法通过。所以得推波式子：

$$\begin{aligned} ans&=\sum_{i=0}^{n} \sum_{j=0}^{a_i-1} f_{i,j}\\ &=\sum_{i=0}^{n} (f_{i,0}+f_{i,1}+\cdots+f_{i,a_i-1})\\ &=\sum_{i=0}^{n} (f_{i+1,0}+f_{i,1}+\cdots+f_{i,a_i-1})\\ &=\sum_{i=0}^{n} (f_{i+1,1}+f_{i,2}+\cdots+f_{i,a_i-1})\\ &=\sum_{i=0}^{n} (f_{i+1,2}+f_{i,3}+\cdots+f_{i,a_i-1})\\ &=\sum_{i=0}^{n} f_{i+1,a_i-1+1}\\ &=\sum_{i=0}^{n} C_{i+a_i}^{i+1} \end{aligned} $$

在推式子的过程中，利用 $f_{x,y}=f_{x-1,y}+f_{x,y-1}$ 不断合并相邻两项即可。还有一种方法是化成组合数求和后裂项。

采用预处理逆元求组合数，复杂度可以做到 $O(n)$。注意 $a_i+i$ 可以到 $4\times 10^{5}$，预处理范围要开大。

:::info[代码]

const int N = 4e5 + 5;
int n, a[N];
mint fac[N], ifac[N];
mint C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] * ifac[n - m]; 
}

void _main() {
	cin >> n;
	for (int i = 0; i <= n; i++) cin >> a[i];
	fac[0] = ifac[0] = 1;
	for (int i = 1; i < N; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	mint res = 0;
	for (int i = 0; i <= n; i++) res += C(i + a[i], i + 1);
	cout << res;
}

:::

CF571A Lengthening Sticks

考虑求合法数目，发现 $a+b>c$ 性质不太好。正难则反，用减法原理，用总数减去不合法的数目。

先求总数。枚举加上的数总和为 $i \in [1,l]$，加到 $3$ 个数上，用插板法，$k$ 个小球之间插 $2$ 块板，方案数为 $C_{i+2}^2$，且 0, 0, 0 也属于总数，故总数

$$1+\sum_{i=1}^{l}C_{i+2}^2=1+\sum_{i=1}^{k}\dfrac{(i+1)(i+2)}{2} $$

再考虑不合法的方案。不妨设 $c$ 为最长边，枚举 $i \in [0,l]$ 分配给 $c$，则 $l-i$ 个数分配给 $a,b$，且要求 $a+b \le c$，所以不合法分配为 $u=\min(c+i-a-b, l-i)$，方案数为 $C^{2}_{u+2}=\dfrac{(u+1)(u+2)}{2}$，加法原理合并方案。然后对于 $a,b$ 为最长边同理。

:::info[代码]

#define int long long
int a, b, c, l;
int solve(int a, int b, int c) {
	int res = 0;
	for (int i = 0; i <= l; i++) {
		int u = min(c + i - a - b, l - i);
		if (u >= 0) res += (u + 1) * (u + 2) / 2;
	} return res;
}

void _main() {
	cin >> a >> b >> c >> l;
	int res = 1;
	for (int i = 1; i <= l; i++) res += (i + 1) * (i + 2) / 2;
	res -= solve(a, b, c), res -= solve(a, c, b), res -= solve(b, c, a);
	cout << res;
} 

:::

CF1929F Sasha and the Wedding Binary Search Tree

BST 题经典套路中序遍历，问题转化为给 $-1$ 赋值使序列单调不降的方案数。进一步地，对于两个已经确定的点 $i,j$，则对 $(i,j)$ 中的数产生限制 $num \in [a_i,a_j]$，于是我们只需解决这个问题：

• 给出一个长为 $n$ 的序列，值域为 $[l,r]$，求让其单调不降的方案数。

很遗憾的是笔者赛时没有做出来。考虑先把第 $i$ 个数加上 $i$，则单调不降转为严格递增。而递增序列直接选出 $n$ 个不同的数即可，值域为 $[l+1,r+n]$，故答案就是 $C_{r-l+n}^{n}$。或者考虑插板法，$n$ 块板子插入 $r-l+n$ 个空也能得出来。

注意 $c$ 很大，直接逆元法会 RE，但 $\sum n \le 10^6$，所以分子可以暴力，仍然处理一下逆元。

:::info[代码]

const int N = 2e6 + 5;
mint fac[N], ifac[N];
mint C(int n, int m) {  
	if (n < m) return 0;
	//return fac[n] * ifac[m] * ifac[n - m]; 
	mint res = 1;
	for (int i = n - m + 1; i <= n; i++) res *= i;
	return res * ifac[m];
} mint solve(int n, int l, int r) {
	if (n <= 0 || l > r) return 1;
	return C(r - l + n, n);
}

int n, c, a[N], ls[N], rs[N], v[N];
void dfs(int rt) {
	if (rt == -1) return;
	dfs(ls[rt]), a[++a[0]] = v[rt], dfs(rs[rt]);
}

void _main() {
	cin >> n >> c;
	for (int i = 1; i <= n; i++) cin >> ls[i] >> rs[i] >> v[i];
	a[0] = 0, dfs(1);
	mint res = 1;
	int l = 0;
	for (int i = 1; i <= n; i++) {
		if (a[i] == -1) continue;
		res *= solve(i - l - 1, l ? a[l] : 1, a[i]);
		l = i;
	}
	res *= solve(n - l, l ? a[l] : 1, c);
	cout << res << '\n';
}

:::

CF1227F2 Wrong Answer on test 233 (Hard Version)

妙妙套路题。考虑单个位置的贡献变化，有 $0$ 变 $1$，$1$ 变 $0$，$0$ 变 $0$，$1$ 变 $1$ 四种情况。由于题目要求 $s'>s$ 的方案数，就只需考虑 $0$ 变 $1$，$1$ 变 $0$ 的情况。而产生变化当且仅当 $h_i$ 与 $h_{i\bmod n+1}$ 不同。若原来的 $a_i=h_i$，移动后就不满足 $a'_{j}=h_{j}$，是 $1$ 变 $0$，而若 $a_i=h_j$，就是 $0$ 变 $1$。通过上述讨论发现：$0$ 变 $1$ 的方案数等于 $1$ 变 $0$ 的方案数。

因此，答案其实就是

$$\dfrac{k^n-p}{2}$$

其中 $p$ 表示分数不变的方案数。现在我们只要算出 $p$ 即可。设有 $m$ 个位置使得 $h_i$ 与 $h_{i\bmod n+1}$ 不同，分数不变就是说移动时对了 $i$ 个，错了 $i$ 个，则 $2i \le m$，即 $i \in [0,\lfloor \dfrac{m}{2} \rfloor]$。枚举 $i$，考察 $i$ 产生的贡献，有三部分：

• 对了 $i$ 个，从 $m$ 个位置选出 $i$ 个，方案数 $C^i_m$；
• 错了 $i$ 个，从剩下 $m-i$ 个位置再选 $i$ 个，然后考虑不同选项，一共是错 $m-2i$ 个，且去掉正确的选项与自身，总方案是 $C^{i}_{m-i} (k-2)^{m-2i}$。
• 除这 $m$ 个以外，其他的可以任意选，方案数 $k^{n-m}$。

由乘法原理合并答案

$$p=\sum_{i=0}^{\lfloor \frac{m}{2} \rfloor}C^i_mC^{i}_{m-i} (k-2)^{m-2i}k^{n-m} $$

注意特判 $k=1$。用逆元法求组合数即可。

:::info[代码]

const int N = 2e5 + 5;
int n, k, a[N];
mint fac[N], ifac[N];
mint C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] * ifac[n - m]; 
}

void _main() {
	cin >> n >> k;
	if (k == 1) return cout << 0, void();
	fac[0] = ifac[0] = 1;
	for (int i = 1; i < N; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	int m = 0;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) {
		if (a[i] != a[i % n + 1]) m++;
	} mint res = 0;
	for (int i = 0; i <= m / 2; i++) res += C(m, i) * C(m - i, i) * mint(k - 2).pow(m - 2 * i) * mint(k).pow(n - m);
	cout << (mint(k).pow(n) - res) / 2;
} 

:::

CF785D Anton and School - 2

考虑枚举子序列的最后一个左括号，可以动态统计其左侧及自身的左括号数目 $a$，右括号数目 $b$，然后枚举再选 $i$ 个括号，则其贡献为

$$\sum_{i=0}^{\min(a-1,b-1)} C_{a-1}^iC_{b}^{i+1}$$

因为括号要匹配，只能枚举到 $\min(a-1,b-1)$，然后考虑组合意义，乘法原理合并两种方案。预处理逆元后复杂度是 $O(n^2)$，无法通过。

根据组合数性质 1，即对称性有

$$\sum_{i=0}^{\min(a-1,b-1)} C_{a-1}^iC_{b}^{i+1}=\sum_{i=0}^{\min(a-1,b-1)} C_{a-1}^{a-1-i}C_{b}^{i+1} $$

然后应用组合数性质 5，即范德蒙恒等式化简

$$\sum_{i=0}^{\min(a-1,b-1)} C_{a-1}^{a-1-i}C_{b}^{i+1}=C_{a+b-1}^a $$

于是逆元法求组合数，复杂度可以为 $O(n)$。

:::info[代码]

const int N = 2e5 + 5;
int n, a[N], b[N];
char s[N];
mint fac[N], ifac[N];
mint C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] * ifac[n - m]; 
}

void _main() {
	cin >> (s + 1); n = strlen(s + 1);
	fac[0] = ifac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	for (int i = 1; i <= n; i++) a[i] = a[i - 1] + (s[i] == '(');
	for (int i = n; i >= 1; i--) b[i] = b[i + 1] + (s[i] == ')');
	mint res = 0;
	for (int i = 1; i <= n; i++) {
		if (s[i] == '(') res += C(a[i] + b[i] - 1, a[i]);
	} cout << res;
} 

:::

P4859 已经没有什么好害怕的了

形式化题意：给出长为 $n$ 的序列 $a,b$，将其两两配对使得 $a_i>b_i$ 的数目减去 $a_i<b_i$ 的数目恰为 $k$，求方案数。

设 $a_i>b_i$ 的数量为 $m$，则 $m-(n-m)=k$，解得 $m=\dfrac{n+k}{2}$。若 $2 \nmid (n+k)$，直接判定无解。此时问题变成 $a_i>b_i$ 的数目恰好为 $m$。考虑使用二项式反演化恰好为钦定。设 $g_i$ 为 $a_i>b_i$ 的组数不小于 $i$ 的方案数，根据二项式反演所求为

$$\sum_{i=m}^{n} (-1)^{i-m} C_{i}^k g_i$$

现在的问题就是求 $g_i$，这玩意很 DP，所以设 $dp_{i,j}$ 表示前 $i$ 个数中选出 $j$ 组 $a_i>b_i$ 的方案数。DP 题套路对 $a,b$ 排序，然后可以推出转移方程

$$dp_{i,j}=dp_{i-1,j}+(last_i-j+1)dp_{i-1,j-1}$$

可以看看下文的排列计数 DP，从插入角度考虑 $(a_i,b_i)$ 的贡献，一种情况是不作为新的 $a_i>b_i$，还有一种就是考虑有多少个取代位置。设 $last_i$ 表示 $b$ 序列中第一个小于 $a_i$ 的数的下标，则插入位置就有 $last_i-j+1$ 个，加法原理合并答案。

于是我们 $O(n^2)$ 求出 $dp_{i,j}$。考察 $g_i$ 的定义可得

$$g_i=dp_{n,i}\times (n-i)!$$

就是在有序的 dp 基础上考虑剩下 $n-i$ 个全排列。

二项式反演中组合数可以逆元法来求，总复杂度 $O(n^2)$。

:::info[代码]

const int N = 2005;
int n, m, k, a[N], b[N], last[N];
mint fac[N], ifac[N], dp[N][N], g[N];
mint C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] * ifac[n - m]; 
}

void _main() {
	cin >> n >> k;
	if ((n + k) & 1) return cout << 0, void();
	fac[0] = ifac[0] = 1;
	for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	
	m = (n + k) / 2;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];
	sort(a + 1, a + n + 1), sort(b + 1, b + n + 1);
	for (int i = 1; i <= n; i++) last[i] = lower_bound(b + 1, b + n + 1, a[i]) - b - 1;
	dp[0][0] = 1;
	for (int i = 1; i <= n; i++) {
		dp[i][0] = dp[i - 1][0];
		for (int j = 1; j <= i; j++) {
			dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] * max(0, last[i] - j + 1);
		}
	}
	for (int i = 0; i <= n; i++) g[i] = dp[n][i] * fac[n - i];
	mint res = 0;
	for (int i = m; i <= n; i++) {
		if ((i - m) & 1) res -= C(i, m) * g[i];
		else res += C(i, m) * g[i];
	} cout << res;
} 

:::

P4345 [SHOI2015] 超能粒子炮·改

组合数前缀和科技的板子。题意还是比较清楚的，就是求

$$f(n,k)=\sum_{i=0}^{k} C_n^i \bmod 2333$$

打个试除法判质数可以发现 $2333$ 是质数，于是这个题适用 Lucas 定理，下面设 $p=2333$，那么

$$f(n,k)=\sum_{i=0}^{k} C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{i}{p} \rfloor} C_{n \bmod p}^{i \bmod p} $$

接着我们把后面的 $C_{n \bmod p}^{i \bmod p}$ 按取模意义考虑贡献，且对于 $\lfloor \dfrac{i}{p} \rfloor$ 进行讨论，则

$$\begin{aligned} f(n,k)&=C_{\lfloor \frac{n}{p} \rfloor}^0 \sum_{i=0}^{p-1} C_{n \bmod p}^i+C_{\lfloor \frac{n}{p} \rfloor}^1 \sum_{i=0}^{p-1} C_{n \bmod p}^i+\cdots+C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p}-1 \rfloor} \sum_{i=0}^{p-1} C_{n \bmod p}^i+C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p} \rfloor} \sum_{i=0}^{k \bmod p} C_{n \bmod p}^i\\ &=(\sum_{i=0}^{p-1} C_{n \bmod p}^i)(C_{\lfloor \frac{n}{p} \rfloor}^0+C_{\lfloor \frac{n}{p} \rfloor}^1 +\cdots+C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p}-1 \rfloor} )+C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p} \rfloor} \sum_{i=0}^{k \bmod p} C_{n \bmod p}^i\\ &=f(n \bmod p,p-1) \times f(\lfloor \dfrac{n}{p} \rfloor, \lfloor \dfrac{k}{p}-1 \rfloor)+C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p} \rfloor} \times f(n \bmod p,k \bmod p) \end{aligned} $$

对于前面的 $n \bmod p$，根据余数性质可得这个东西小于 $p$，所以我们可以直接 $O(p^2)$ 地递推法求出。对于 $\dfrac{n}{p}$，$n$ 每次至少除掉 $p$，复杂度级别为 $O(\log n)$。最后的 $C_{\lfloor \frac{n}{p} \rfloor}^{\lfloor \frac{k}{p} \rfloor}$ 可以用 Lucas 定理法求出。预处理 $O(p^2)$，单次查询 $O(\log (n+k))$，但由于这个对数的底数为 $p=2333$，可以直接当作小常数。

:::info[代码]

const int N = 2400, p = 2333;
long long q, n, k;
mint c[N][N], pre[N][N];

mint lucas(long long n, long long m) {
	if (n < m) return 0;
	if (n == m) return 1;
	return c[n % p][m % p] * lucas(n / p, m / p);
}
mint f(long long n, long long k) {
	if (k < 0) return 0;
	if (n == 0 || k == 0) return 1;
	if (n < p && k < p) return pre[n][k];
	return f(n / p, k / p - 1) * pre[n % p][p - 1] + pre[n % p][k % p] * lucas(n / p, k / p);
} 

void _main() {
	for (int i = 0; i < N; i++) c[i][0] = 1, c[i][i] = 1;
	for (int i = 0; i < N; i++) {
		for (int j = 1; j < i; j++) c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
	}
	for (int i = 0; i < N; i++) {
		pre[i][0] = 1;
		for (int j = 1; j < N; j++) pre[i][j] = pre[i][j - 1] + c[i][j];
	}
	for (cin >> q; q--; ) cin >> n >> k, cout << f(n, k) << '\n';
}

:::

错位排列

错排数 $D_i$ 是指将 $1$ 到 $n$ 的自然数排列重新排列为 $P_i$ 后，满足 $\forall i \in [1,n], P_i \ne i$ 的方案数。

例如，$n=3$ 时，错位排列有 $\{2,3,1\}$ 和 $\{3,1,2\}$。

递推公式

计算错排数可以递推。考虑 $D_n$ 时，先把 $n$ 放在 $P_n$，然后有两种情况：

1. 前面 $n-1$ 个数已经是错位排列；
2. 前面 $n-1$ 个数有一个在原位上，其他错位。

对于情况 1，第 $n$ 个数可以与任一数字交换，有 $(n-1)D_{n-1}$ 种方案；

对于情况 2，第 $n$ 个数只能与原位上的交换，有 $(n-1)D_{n-2}$ 种方案；

因此，

$$D_n=(n-1)(D_{n-1}+D_{n - 2})$$

另外地，$D_1=0,D_2=1$。

对 $D_n=(n-1)(D_{n-1}+D_{n - 2})$ 变形：

$$\begin{aligned} D_n&=(n-1)(D_{n-1}+D_{n - 2})\\ D_n&=(n-1)D_{n-1}+(n-1)D_{n-2}\\ D_n-nD_{n-1}&=-D_{n-1}+(n-1)D_{n-2}\\ D_n-nD_{n-1}&=(-1)(D_{n-1}-(n-1)D_{n-2}) \end{aligned} $$

由此可见 $D_n-nD_{n-1}$ 是首项为 $1$，公比为 $-1$ 的等差数列，由此可得错排的另一个递推式

$$D_n=nD_{n-1}+(-1)^n$$

通项公式

由递推式 2，两边同时除以 $n!$ 有

$$\dfrac{D_n}{n!}=\dfrac{D_{n-1}}{(n-1)!}+\dfrac{(-1)^n}{n!} $$

根据递推式不断代入，累加：

$$\dfrac{D_n}{n!}=\sum_{k=0}^{n} \dfrac{(-1)^k}{k!}$$

因此可得错排通项公式

$$D_n=n!\sum_{k=0}^{n} \dfrac{(-1)^k}{k!}$$

范围估计

根据通项公式可以估计错排的增长速度。由式子

$$\dfrac{D_n}{n!}=\sum_{k=0}^{n} \dfrac{(-1)^k}{k!}$$

可以想到 $e^{-1}$ 的泰勒展开。写出 $\dfrac{1}{e}$ 在 $x=-1$ 处的泰勒展开：

$$\dfrac{1}{e}=\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k!} $$

因此：

$$\dfrac{1}{e}=\dfrac{D_n}{n!} + \sum_{k=n+1}^{\infty} \dfrac{(-1)^k}{k!} $$

注意到，当 $n$ 增加时，后面的和式趋近于 $0$，因此可得错排数列的极限：

$$\lim_{n \to +\infty} D_n=\dfrac{n!}{e}$$

即 $D_n=O(n!)$。因此在复杂度中用到错排时，可认为它是阶乘级别的。

例题

P1595 信封问题

板子题。

:::info[代码]

const int N = 25;
int n;
long long d[N];

void _main() {
	d[2] = 1;
	for (int i = 3; i < N; i++) d[i] = (i - 1) * (d[i - 1] + d[i - 2]);
	cin >> n;
}

:::

P4071 [SDOI2016] 排列计数

稍微思考一下就能发现，可以先选出 $m$ 个数，使得 $a_i=i$，然后再让剩下 $n-m$ 个数都满足 $a_i \ne i$，这就是错排数 $D_{n-m}$。因此答案即为 $C_{n}^{m} \times D_{n-m}$。采用预处理逆元的方法求组合数即可。

:::info[代码]

const int N = 1e6 + 5;
const long long mod = 1e9 + 7;
long long d[N], fac[N], ifac[N];

long long power(long long a, long long b) {
	long long res = 1;
	for (a %= mod; b; b >>= 1) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}

long long t, n, m;

void _main() {
	d[2] = 1;
	for (int i = 3; i < N; i++) d[i] = 1LL * (i - 1) * ((d[i - 1] + d[i - 2]) % mod) % mod;
	
	fac[0] = 1;
	for (int i = 1; i < N; i++) {
		fac[i] = fac[i - 1] * i % mod;
		ifac[i] = power(fac[i], mod - 2);
	}
	for (cin >> t; t--; ) {
		cin >> n >> m;
		if (m == 0) {cout << d[n] << '\n'; continue;}
		if (n == m) {cout << 1 << '\n'; continue;}
		if (n == m + 1) {cout << 0 << '\n'; continue;}
		cout << (fac[n] * ifac[m] % mod * ifac[n - m] % mod) * (n >= m ? d[n - m] : 1) % mod << '\n';
	}
}

:::

同样的思想可以解决 P8788 的问题 A。

Catalan 数

Catalan 数的起源是凸多边形三角剖分问题，即对于一个凸 $n$ 边形，有多少种方式可以用不相交的对角线将其划分为若干个三角形。这里将方案数记作 $H_n$。Catalan 数列为：
$1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862\cdots$

解决问题

1. 括号序列计数

Q: 计算 $n$ 对括号能形成多少种合法括号序列。

A: 方案数为 $H_n$。因为序列的第一个括号必须为 (，设之后有一个长度为 $m$ 的子序列，然后为 )，再然后是另一个子序列，长度为 $n-m-1$，则方案为 $H_n=\sum_{m=0}^{n-1} H_i H_{n-m-1}$，这就是 Catalan 的递推式。

2. 不同构二叉树计数

Q: 计算 $n$ 个节点的不同构二叉树数目。

A: 数目为 $H_n$。设根节点左子树大小为 $m$，则右子树大小为 $n-m-1$，左右子树又是一个子问题，所以方案为 $H_n=\sum_{m=0}^{n-1} H_i H_{n-m-1}$，符合递推式。

3. 三角剖分问题

Q: 求对于一个凸 $n$ 边形，有多少种方式可以用不相交的对角线将其划分为若干个三角形。

A: 方案数为 $H_n$。固定多边形的一条边并选择一个与它不共线的初始顶点构成一个三角形，这个三角形将原多边形分为两个小多边形，大小分别为 $m$ 和 $n-m-1$，所以方案还是那个 $H_n=\sum_{m=0}^{n-1} H_i H_{n-m-1}$。

4. 不越过对角线的网格路径

Q: 在 $n \times n$ 网格中，从 $(0,0)$ 走到 $(n,n)$ 且只能向右或向上移动，求不越过对角线 $y=x$ 的路径数，如图所示。

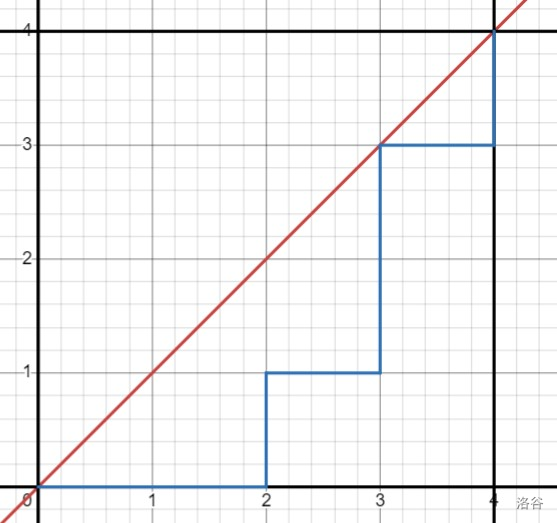
A: 路径数为 $H_n$。如果你不考虑限制，就是在总共 $2n$ 步中分出 $n$ 步走上或者右，总之方案数为 $C_{2n}^{n}$。用减法原理，算不合法的方案，则不合法路径的终点是 $(n-1,n+1)$，选出 $n-1$ 步走右，方案数 $C_{2n}^{n-1}$，因此答案为 $C_{2n}^n-C_{2n}^{n-1}$。这是 Catalan 数的通项公式。

5. 出栈序列计数

Q: 入栈序列为一个 $1$ 到 $n$ 的排列，求合法出栈序列数目。

A: 数目为 $H_n$。设第一个入栈元素在第 $m$ 个出栈，则前面 $m-1$ 个必须在之前出入栈，而之后又 $n-m-1$ 种，递推式又双叒叕是 $H_n=\sum_{m=0}^{n-1} H_i H_{n-m-1}$。

由此可见，能用 Catalan 数解决的问题都满足一个递归分解结构：一个大小为 $n$ 的问题可以分解为两个独立子问题，规模分别为 $m$ 与 $n-m-1$，且两子问题分步，也就是用乘法原理组合。

计算公式

上面已经给出了一个递推式：

$$H_n=\sum_{i=0}^{n-1} H_{i-1} H_{n-i}$$

还有一个递推式：

$$H_n=\dfrac{H_{n-1}(4n-2)}{n+1}$$

根据问题 4 可知通项公式：

$$H_n=\dfrac{C_{2n}^n}{n+1}=C_{2n}^n-C_{2n}^{n-1}$$

使用递推式可以在 $O(n)$ 复杂度内预处理 $H_i$。而使用通项公式再用 lucas / exLucas 等科技则可以获得更低的复杂度。

例题

P1044 [NOIP 2003 普及组] 栈

就是问题 5。用递推式 2 计算即可。

:::info[代码]

long long n, h[20];

void _main() {
	cin >> n;
	h[0] = 1;
	for (int i = 1; i <= n; i++) h[i] = h[i - 1] * (4 * i - 2) / (i + 1);
	cout << h[n];
}

:::

P1375 小猫

题目描述有点抽象，其实就是一个多边形三角剖分问题，所以方案数还是 Catalan 数。代码和上题的区别就是加个取模。

双倍经验：P1976。

P10413 [蓝桥杯 2023 国 A] 圆上的连线

这题可以不连线，所以先从 $2023$ 个点选 $n$ 个设为必须连边，这一步方案为 $C_{2023}^n$。

然后这个问题就是上一题，答案为 $H_{n/2}$。由乘法原理可得答案，注意 $n$ 是偶数。

$$\sum_{n=0}^{2023} C_{2023}^{n} H_{n/2}, n \in \{2x | x \in \mathbb{\N^+} \} $$

考虑到 $2023$ 不是质数，你应该对组合数和 Catalan 数都用递推来求解。答案是 $104$。

P1754 球迷购票问题

先审题，当 A 买票后，售票处得到一个 $50$ 元；当 B 买票后，售票处失去一个 $50$ 元，所以 A, B 是一个二元对应关系。建立括号模型，将 A 当作左括号，B 当作右括号，发现合法的排队序列就是括号匹配序列，这是问题 1，还是写 Catalan 数即可。

P2532 [AHOI2012] 树屋阶梯

把这题放 Catalan 数例题说明了一切。

用 $f_i$ 表示高度为 $i$ 的阶梯的搭建方案数，显然 $f_0=f_1=1$。借用一下第一篇题解的图：

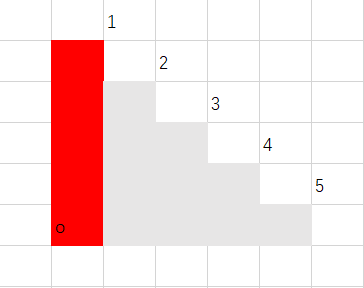
枚举每个顶到拐角的矩形，比如这里的第一个矩形，那么右侧方案是 $f_4$。

再看这个矩形，上侧为 $f_1$，右侧为 $f_3$。

类似地，上侧为 $f_2$，右侧为 $f_2$。同理可得另外的情况，因此

$$f_n=\sum_{i=0}^{n-1} f_{i} f_{n-i-1}$$

这满足“一个大小为 $n$ 的问题可以分解为两个独立子问题，规模分别为 $m$ 与 $n-m-1$，且两子问题分步”的条件，所以所求就是 Catalan 数。然后你整个高精度即可，代码不放了。

P3978 [TJOI2015] 概率论

首先由问题 2 可得不同构二叉树有 $H_n$ 棵。然后设 $f_n$ 表示所有二叉树的叶子节点数目之和。

注意到，$f_n=nH_{n-1}$。

简证：对于一棵 $n$ 个节点的二叉树，若存在 $k$ 个叶子节点，将 $k$ 个叶子依次删去，可构造得 $k$ 棵 $n-1$ 个点的二叉树，并且这些二叉树还有 $n$ 个点可以挂叶子，因此 $f_n =\sum k H_{n-1}=nH_{n-1}$。

然后期望为 $E(X)=\dfrac{f_n}{H_n}$，代入通项公式 $H_n=\dfrac{C_{2n}^n}{n+1}$ 消去可得 $E(X)=\dfrac{n(n+1)}{2(2n-1)}$。于是这道紫题就做完了。

P7118 Galgame

根据问题 2，节点数小于 $n$ 的二叉树数目为

$$\sum_{i=1}^{n-1} H_i$$

重点是算节点数相同的二叉树。根据先左再右的比较方式，设左儿子大小为 $s$，左右儿子总大小为 $n$，和问题 2 相同的推导方法可得方案数是

$$\sum_{i=0}^{s-1} H_{i} H_{n-i-1}$$

预处理 Catalan 数，在 dfs 过程中记录乘子，如果走了左链，右子树就不用管了可以任意选，因此由乘法原理将乘子乘上右子树大小，具体细节看代码。

:::info[代码]

const int N = 2e6 + 5;
int n, ls[N], rs[N], sz[N];
mint h[N];

void dfs1(int u) {
	if (!u) return;
	dfs1(ls[u]), dfs1(rs[u]), sz[u] = sz[ls[u]] + sz[rs[u]] + 1;
} mint dfs2(int u, mint x) {
	if (!u) return 0;
	mint res = 0;
	for (int i = 0; i < sz[ls[u]]; i++) res += x * h[i] * h[sz[u] - i - 1];
	res += dfs2(ls[u], x * h[sz[rs[u]]]);
	res += dfs2(rs[u], x);
	return res;
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> ls[i] >> rs[i];
	h[0] = 1;
	for (int i = 1; i <= (n << 1); i++) h[i] = h[i - 1] * (4 * i - 2) / (i + 1);
	mint res = 0;
	for (int i = 1; i < n; i++) res += h[i];
	dfs1(1), res += dfs2(1, 1);
	cout << res;
} 

:::

喜提 30pts 大黑大紫。因为这样做是 $O(n^2)$ 的，会被左偏形态的树卡满。

考虑当左子树大小大于右子树时，用右子树大小代替左子树大小计算。用减法原理，用总方案数减去不小于原树的二叉树。记右子树大小为 $s$，同理可得答案

$$H_n-\sum_{i=0}^{s} H_{i}H_{n-i-1}$$

然后你神奇地发现这变成了启发式合并，复杂度是 $O(n \log n)$ 的。然后你把 dfs2 改成这样即可：

:::info[代码]

mint dfs2(int u, mint x) {
	if (!u) return 0;
	mint res = 0;
	if (sz[ls[u]] <= sz[rs[u]]) {
		for (int i = 0; i < sz[ls[u]]; i++) res += x * h[i] * h[sz[u] - i - 1];
	} else {
		res += x * h[sz[u]];
		for (int i = 0; i <= sz[rs[u]]; i++) res -= x * h[i] * h[sz[u] - i - 1];
	}
	res += dfs2(ls[u], x * h[sz[rs[u]]]);
	res += dfs2(rs[u], x);
	return res;
}

:::

Stirling 数

第二类 Stirling 数

第二类 Stirling 数 $S(n,k)$ 表示将 $n$ 个不同元素分为 $k$ 个互不区分的非空子集的方案数。

第二类 Stirling 数有递推计算和通项计算两种计算方法。

递推公式

考虑到第 $n$ 个元素时，有两种方案：

1. 将第 $n$ 个元素单独放一个新子集，方案数为 $S(n-1,k-1)$；
2. 将第 $n$ 个元素放一个已有子集，方案数为 $k \times S(n-1,k)$。

由加法原理得：

$$S(n,k)=S(n-1,k-1)+k \times S(n-1,k)$$

通项公式

$$S(n,k)=\sum_{i=0}^{k} \dfrac{(-1)^{k-i} i^n}{i!(k-i)!} $$

::::success[证明]

发现这个东西长的像二项式反演的式子，故设将 $n$ 个不同元素划分到 $i$ 个不同可空集合的方案数为 $g_i$，将 $n$ 个不同元素划分到 $i$ 个不同非空集合的方案数为 $g_i$。由乘法原理易得

$$g_i=i^n$$

枚举选出多少个元素 $j$，则

$$g_i=\sum_{j=0}^{i} C_i^j f_j$$

这是二项式反演的标准形式。由二项式反演

$$\begin{aligned} f_i&=\sum_{j=0}^{i} (-1)^{i-j} C_i^j g_j\\ &=\sum_{j=0}^{i} (-1)^{i-j} C_i^j j^n\\ &=\sum_{j=0}^{i} \dfrac{i!(-1)^{i-j}j^n}{j!(i-j)!} \end{aligned} $$

得到了 $f_i$ 的通项公式。因为 $S(n,i)$ 中的子集互不区分，所以 $f_i$ 在 $S(n,i)$ 的基础上作了全排列，即 $f_i=i! \times S(n,i)$，所以

$$S(n,k)=\dfrac{f_k}{k!}=\sum_{i=0}^{k} \dfrac{(-1)^{k-i} i^n}{i!(k-i)!} $$

::::

第一类 Stirling 数

第一类 Stirling 数 $s(n,k)$ 表示将 $n$ 个不同元素分为 $k$ 个互不区分的非空环形排列的方案数。

第一类 Stirling 数可通过递推计算。考虑到第 $n$ 个元素时，仍有两种方案：

1. 将第 $n$ 个元素单独放一个新环，方案数为 $s(n-1,k-1)$；
2. 将第 $n$ 个元素放一个已有环，方案数为 $(n-1) \times s(n-1,k)$。

由加法原理得：

$$s(n,k)=s(n-1,k-1)+(n-1) \times s(n-1,k)$$

例题

P1655 小朋友的球

这是第二类 Stirling 数的板子，但是需要高精度。

:::info[代码]

const int N = 105;
int n, m;
BigInteger s[N][N];

void _main() {
	s[0][0] = 1;
	for (int i = 1; i < N; i++) {
		for (int j = 1; j <= i; j++) {
			s[i][j] = s[i - 1][j - 1] + s[i - 1][j] * j;
		}
	}
	while (cin >> n >> m) {
		cout << s[n][m] << '\n';
	}
}

:::

B3801 [NICA #1] 乘只因

题里给的条件就是：

$$\prod_{i=1}^{k} a_i = \operatorname{lcm}_{i=1}^{k} a_i =n $$

因为 $\operatorname{lcm}_{i=1}^{k}=\dfrac{\prod_{i=1}^{k} a_i}{\gcd_{i=1}^{k} a_i}$，所以 $\gcd_{i=1}^{k} a_i=1$，而且又说了 $a$ 单调不降，就是说 $a$ 序列两两互质。对 $n$ 分解质因数得 $n=p_1^{a_1} p_2^{a_2} \cdots$，发现若 $a_x \ne 0$，则这些 $p_x$ 只能被分配到同一个 $a_i$ 中。记有 $c$ 个不同质因子，然后你发现这是把 $c$ 个元素划成 $k$ 个子集的方案数，即第二类 Stirling 数。

实现细节上，注意特判掉 $c<k$ 的情况。

:::info[代码]

int n, k;
int decompose(int n) {
	int m = 0;
	for (int i = 2; i * i <= n; i++) {
		if (n % i) continue;
		m++;
		while (n % i == 0) n /= i;
	}
	if (n > 1) m++;
	return m;
}

long long s[15][15];

void _main() {
	cin >> n >> k;
	int m = decompose(n);
	cout << (m < k ? 0 : s[m][k]) << '\n';
} signed main() {
	s[0][0] = 1;
	for (int i = 1; i < 15; i++) {
		for (int j = 1; j <= i; j++) {
			s[i][j] = s[i - 1][j - 1] + s[i - 1][j] * j;
		}
   }
	int t = 1; for (cin >> t; t--; ) _main();
}

:::

P4609 [FJOI2016] 建筑师

单调栈经典模型。 首先高度为 $n$ 的建筑肯定不会被挡，用它将建筑划分为两段，左边的看不到右边，右边的看不到左边。

推广一下，把 $n$ 的建筑分成 $a+b-1$ 个部分，把一个可以看到的和被它的分到一组去，一共是 $a+b-2$ 组。我们发现，每一组除了最高的建筑都可以任意排列，而且这还是一个环形排列，所以方案数是第一类 Stirling 数 $s(n-1,a+b-2)$。

然后再思考每一组的放置方法，这是一个组合数 $C_{a+b-2}^{a-1}$。由乘法原理合并答案。

:::info[代码]

int q, n, a, b;
const int N = 205;
mint c[N][N], s[50005][N];

void _main() {
	s[0][0] = 1;
	for (int i = 1; i < 50005; i++) {
		for (int j = 1; j < N; j++) s[i][j] = s[i - 1][j - 1] + s[i - 1][j] * (i - 1);
	}
	for (int i = 0; i < N; i++) c[i][0] = 1, c[i][i] = 1;
	for (int i = 0; i < N; i++) {
		for (int j = 1; j < i; j++) c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
	}
	for (cin >> q; q--; ) {
		cin >> n >> a >> b;
		cout << s[n - 1][a + b - 2] * c[a + b - 2][a - 1] << '\n';
	}
}

:::

Bell 数

Bell 数 $B_n$ 表示大小为 $n$ 的集合的划分方法数。例如，对于集合 $\{1,2,3\}$，有 $5$ 种划分方法：

{1},{2},{3}
{1,2},{3}
{1,3},{2}
{1},{2,3}
{1,2,3}

所以 $B_3=5$。

递推公式

设 $B_n$ 对应集合 $\{a_1,a_2,a_3,\cdots,a_n\}$，$B_{n+1}$ 对应集合 $\{a_1,a_2,a_3,\cdots,a_n,a_{n+1}\}$，只需考虑元素 $a_{n+1}$ 的贡献。

当它和 $k$ 个元素分到一个子集时，还剩下 $n-k$ 个元素，则多出的方案数有 $C_{n}^{n-k} B_{n-k}$，且 $k \in [0,n]$。因此：

$$B_{n+1}=\sum_{k=0}^{n} C_n^k B_k$$

仿照杨辉三角，可以构造一个贝尔三角形：

• $a_{0,0}=1$；
• $a_{n,0}=a_{n-1,n-1}$；
• $a_{n,m}=a_{n,m-1}+a_{n-1,m-1}$。

此时 $B_n=a_{n,0}$。

:::info[实现]

int b[N][N];
void pre() {
  b[0][0] = 1;
  for (int i = 1; i < N; i++) {
    b[i][0] = b[i - 1][i - 1];
    for (int j = 1; j <= i; j++) b[i][j] = b[i - 1][j - 1] + b[i][j - 1];
  }
}

:::

与第二类 Stirling 数的关系

枚举划分成 $k$ 个非空集合，则每种情况的方案数为第二类 Stirling 数 $S(n,k)$。于是：

$$B_n=\sum_{k=0}^n S(n,k)$$

这表明：Bell 数 $B_n$ 就是第 $n$ 行第二类 Stirling 数的和。

例题

CF568B Symmetric and Transitive

做一个图论建模。由对称性可得这是一个无向图，不妨设图中存在 $i$ 个孤立点，则选出孤立点的方案数是 $C_n^i$。然后剩下的分配就是上面讲的集合划分问题，为 $B_{n-i}$。由加法、乘法原理可得所求为

$$\sum_{i=1}^{n} C_n^i B_{n-i}$$

然后组合数用杨辉三角，Bell 数用 Bell 三角预处理即可。

:::info[代码]

const int N = 4005;
int n;
mint b[N][N], c[N][N];

void _main() {
	cin >> n;
	b[0][0] = 1;
	for (int i = 1; i <= n; i++) {
		b[i][0] = b[i - 1][i - 1];
		for (int j = 1; j <= i; j++) b[i][j] = b[i - 1][j - 1] + b[i][j - 1];
	}
	for (int i = 0; i <= n; i++) c[i][0] = 1, c[i][i] = 1;
	for (int i = 0; i <= n; i++) {
		for (int j = 1; j < i; j++) c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
	}
	mint res = 0;
	for (int i = 1; i <= n; i++) res += c[n][i] * b[n - i][0];
	cout << res;
}

:::

分拆数

本来我不打算讲这个，但是 7.22 的模拟赛 T4 就是分拆数板子，并且我还没做出来。

定义分拆：将自然数 $n$ 写为递降正整数和的表示。如 $8=5+2+1$。

分拆数 $p_n$：自然数 $n$ 的分拆方法数。

$k$ 部分拆数

将自然数 $n$ 分成恰好有 $k$ 个部分的分拆，称作 $k$ 部分拆数，记作 $p(n,k)$。如 $9=6+2+1$ 是 $9$ 的一个 $3$ 部分拆。

考虑转移方程。

1. 单独分出一个 $1$，此时剩下数的和为 $n-1$，分 $k-1$ 组；
2. 不选 $1$，不妨把每个数都减去 $1$ 转化为选 $1$ 的方案数，为 $n-k$ 分 $k$ 组。

由加法原理得

$$p(n,k)=p(n-1,k-1)+p(n-k,k)$$

边界为 $p(i,1)=p(i,i)=1$。

:::info[实现]

int n, k;
mint dp[N][N];

void _main() {
	cin >> n >> k;
	for (int i = 1; i <= n; i++) dp[i][1] = dp[i][i] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 2; j <= i; j++) {
			dp[i][j] = dp[i - 1][j - 1] + dp[max(i - j, 0)][j];
		}
	} cout << dp[n][k];
}

:::

并且易得

$$p_n=\sum_{k=1}^{n} p(n,k)$$

最大 $k$ 分拆数

最大 $k$ 分拆数：自然数 $n$ 的最大分拆部分为 $k$ 的方法数。可以证明，最大 $k$ 分拆数等于 $p(n,k)$。

互异分拆数

互异分拆数 $pd_n$：自然数 $n$ 分拆成互不相同的数字的方法数。

同理地，定义 $pd(n,k)$ 表示 $n$ 分成 $k$ 个部分的互异分拆。考虑递推式，将所有数都减去 $k$，由于互异，数字中应当只有 $k$ 或 $k-1$ 个非零数，此时是对 $n-k$ 互异分拆的方案数，由加法原理得

$$pd(n,k)=pd(n-k,k)+pd(n-k,k-1)$$

并且易得

$$pd_n=\sum_{k=1}^{n} pd(n,k)$$

奇分拆数

奇分拆数 $po_n$：自然数 $n$ 分拆成奇数的方法数。利用某些神奇方法，可以证明：

$$po_n=pd_n$$

但是 $k$ 部奇分拆数不是 $k$ 部互异分拆数。

五边形数定理

有结论：

$$p_n=p_{n-1}+p_{n-2}-p_{n-5}-p_{n-7} +p_{n-12}+p_{n-15}-p_{n-22}- \cdots $$

认为负数的分拆数为 $0$。

像这张图一样，五边形数就是能够排列成正五边形的点数。这里的递推式系数 $1,2,5,7, 12,15,22\cdots$ 的通项公式为 $a_{2i}=\dfrac{i(3i-2)}{2}$，而五边形数的通项为 $\dfrac{n(3n-1)}{2}$，所以这个东西叫做五边形数定理，需要用生成函数的方法证明。它的更一般规律是，系数递推式满足 $a_{2i}=\dfrac{i(3i-2)}{2},a_{2i+1}=\dfrac{i(3i+1)}{2}$，若 $4 \mid i$ 则符号为减号，否则为加号。利用五边形数定理可以 $O(n\sqrt{n})$ 计算分拆数。

:::info[实现]

const int N = 1e5 + 5;
long long n, a[N << 1];
mint p[N];   

void _main() {
	p[0] = 1, p[1] = 1, p[2] = 2;
	for (int i = 1; i < N; i++) {
		a[i << 1] = i * (i * 3 - 1) / 2;
		a[i << 1 | 1] = i * (i * 3 + 1) / 2;
	}
	for (int i = 3; i < N; i++) {
		p[i] = 0;
		for (int j = 2; a[j] <= i; j++) {
			if (j & 2) p[i] += p[i - a[j]];
			else p[i] -= p[i - a[j]];
		}
	}
	while (cin >> n, n != -1) cout << p[n] << endl;
} 

:::

排列计数问题

这一部分不属于组合数学内容，而是属于 DP 内容，但其思想方法与推导错排数、Stirling 数和 Bell 数有异曲同工之妙。

这类题目的 dp 状态一般设 $dp_{i, \cdots}$ 表示当前需要放入第 $i$ 个数的方案数，然后根据需要添加维度。在转移时，往往要从插入角度分类讨论 $i$ 带来的贡献，并根据乘法或加法原理合并答案。

例题

P2401 不等数列

观察数据范围可以发现是一个 $O(nk)$ 的 dp，设 $dp_{i,j}$ 表示当前需要放入数字 $i$，有 $j$ 个小于号的方案数。分类讨论：

1. 若放在最左边，会多一个大于号，从 $dp_{i-1,j}$ 转移；
2. 若放在最右边，会多一个小于号，从 $dp_{i-1,j-1}$ 转移；
3. 若插入到小于号之前，因为数字 $i$ 是最大的，所以小于号变为大于号，而前面是一个小于号，因此是多了一个大于号，从 $j \times dp_{i-1,j}$ 转移；
4. 若插入到大于号之前，同理可得转移为 $(i-j-1) \times dp_{i-1,j-1}$。

由加法原理得：

$$dp_{i,j}=(j+1) \times dp_{i-1,j} +(i-j) \times dp_{i-1,j-1} $$

至此本题在 $O(nk)$ 内解决。边界为 $dp_{i,0}=1$。

:::info[代码]

const int N = 1005;
int n, k;
mint dp[N][N];

void _main() {
	cin >> n >> k;
	dp[1][0] = 1;
	for (int i = 2; i <= n; i++) {
		dp[i][0] = 1;
		for (int j = 1; j <= min(i, k); j++) {
			dp[i][j] = dp[i - 1][j] * (j + 1) + dp[i - 1][j - 1] * (i - j);
		}
	} cout << dp[n][k];
}

:::

P6323 [COCI 2006/2007 #4] ZBRKA

还是设 $dp_{i,j}$ 表示当前需要放入数字 $i$，有 $j$ 个逆序对的方案数。考虑插入在 $i-1$ 的全排列中插入 $i$ ，枚举增加了多少逆序对 $k$，则有

$$dp_{i,j} = \sum_{k=0}^{\min(i-1,j)} dp_{i-1,j-k}$$

直接做是 $O(nk^2)$ 的。注意到 $dp_{i,j}$ 为同一行 $dp_{i-1}$ 连续区间的和，用前缀和优化即可。考虑求 $j-k$ 的范围，发现 $j-k \in [\max(0, j-i+1), j]$。边界是 $dp_{i,0}=1$。

:::info[代码]

const int N = 1e3 + 5;
int n, k;
mint dp[N][10005], pre[N];

void _main() {
	cin >> n >> k;
	dp[1][0] = 1;
	fill(pre + 1, pre + k + 2, 1);
	for (int i = 2; i <= n; i++) {
		for (int j = 1; j <= k; j++) dp[i][j] = pre[j + 1] - pre[max(0, j - i + 1)];
		pre[0] = 0;
		for (int j = 1; j <= k; j++) pre[j + 1] = pre[j] + dp[i][j];
	}
	cout << dp[n][k];
}

:::

三倍经验：P1521、P2513。

P7967 [COCI 2021/2022 #2] Magneti

好像这种问题叫做连续段 dp。

DP 题套路先对 $r_i$ 排序简化问题。仍然设 $dp_{i,\cdots}$ 表示当前需要放入第 $i$ 个磁铁的方案数。考虑加维，经过尝试发现空位要是单独一维，连通块也是单独一维。这里的连通块是一个磁铁的排列。因此，设 $dp_{i,j,k}$ 表示当前需要放入第 $i$ 个磁铁，分成 $j$ 个连通块，占用掉 $k$ 个空位的方案数。

考虑插入 $i$ 并分类讨论：

1. 若第 $i$ 个磁铁单独成为新的块，则从 $dp_{i-1,j-1,k-1}$ 转移；
2. 若第 $i$ 个磁铁放在第 $j$ 个连通块端点，则从 $2j \times dp_{i-1,j,k-r_i}$ 转移。
3. 若第 $i$ 个磁铁将两个连通块合并为一个，则从 $j(j+1) \times dp_{i-1,j+1, k-2r_i+1}$ 转移。

于是状态转移方程为：

$$dp_{i,j,k}=dp_{i-1,j-1,k-1}+2j \times dp_{i-1,j,k-r_i}+j(j+1) \times dp_{i-1,j+1, k-2r_i+1} $$

由此可以求出所有磁铁只形成一个连通块且长度为 $i$ 的方案数 $dp_{n,1,i}$，则根据插板法，答案为

$$\sum_{i=1}^{l} dp_{n,1,i} \times C_{l-i+n}^{n}$$

时空 $O(n^2l)$，使用逆元法求组合数。边界为 $dp_{0,0,0}=1$。

:::info[代码]

const int N = 1e4 + 5;
mint fac[N], ifac[N], dp[55][55][N];

mint C(int n, int m) {
	if (n < m) return 0;
	return fac[n] * ifac[m] * ifac[n - m]; 
}

int n, l, r[N];

void _main() {
	fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
	for (int i = 2; i < N; i++) fac[i] = fac[i - 1] * i, ifac[i] = ~fac[i];
	cin >> n >> l;
	for (int i = 1; i <= n; i++) cin >> r[i];
	sort(r + 1, r + n + 1);
	dp[0][0][0] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			for (int k = 1; k <= l; k++) {
				dp[i][j][k] = dp[i - 1][j - 1][k - 1];
				if (k >= r[i]) dp[i][j][k] += dp[i - 1][j][k - r[i]] * 2 * j;
				if (k >= 2 * r[i] - 1) dp[i][j][k] += dp[i - 1][j + 1][k - 2 * r[i] + 1] * j * (j + 1);
			}
		}
	}
	mint res = 0;
	for (int i = 1; i <= l; i++) res += dp[n][1][i] * C(l - i + n, n);
	cout << res;
}

:::

位运算

本来不打算讲的，但是发现 OI 里位运算的题也不少，所以开个新专题。

下文用符号 $\oplus$ 表示按位异或，$\&$ 表示按位与，$|$ 表示按位或。

位运算常用性质

1. 由于异或是不进位加法，不退位减法，故 $x-y \le x \oplus y \le x + y$。
2. 按位考虑 $x,y$ 的异同，有 $x+y=(x\& y) +(x|y)$。
3. 异或是不进位加法，而 $2(x \& y)$ 又能够表示加法进位，因此 $x+y=(x \oplus y)+2(x \& y)$。
4. 对于常数 $x,n$，满足 $x \oplus i \le n$ 的 $i$ 形成的区间有 $O(\log n)$ 个。

位运算进阶

位运算基础就不讲了。让我们来考虑下列问题：

1. 定义 $\operatorname{lowbit}(x)$ 为 $x$ 最低位的 $1$ 及后面的 $0$ 组成的数。如何计算 $\operatorname{lowbit}(x)$ ？

A: 将 $x$ 二进制位全部取反再加一。设原来 $x$ 的二进制表示形如 (...)10...0000，全部取反可得 [...]01...1111，加一即为 [...]10...0000，且 [...] 与 (...) 内容全部相反，两数或之，得 $10...0000$，即 $\operatorname{lowbit}(x)$。由补码性质可得 ~x + 1 = -x，因而代码可以这样写：

constexpr int lowbit(int x) {return x & -x;}

这个函数在树状数组中有大用。还有一种方法是 $x-\operatorname{lowbit}(x)=x\& (x-1)$。

2. 定义 $\operatorname{popcount}(x)$ 为二进制下 $x$ 中 $1$ 的个数，如何计算 $\operatorname{popcount}(x)$？

A: 考虑每次减去它的 $\operatorname{lowbit}$，复杂度 $O(\log n)$。

:::info[实现]

int popcount(int x) {
	int res = 0;
	for (; x; x -= lowbit(x)) res++;
	return res;
}

:::

GNU C++ 提供了函数 __builtin_popcount(x)，这个函数的速度远快于上面代码，可视为 $O(1)$。另有函数 __builtin_popcountll(x) 来计算 long long 类型的 $\operatorname{popcount}$。

3. 使用一个 $n$ 位的二进制整数 $s$ 压位表示一个集合，如何降序枚举其子集？

A: 先上代码：

for (int i = s; i; i = (i - 1) & s);

降序获得下一个子集，其实就是将它的最低位 $1$ 置为 $0$，减去 $1$ 即可，但是这会导致其最低位的 $1$ 后所有的 $0$ 变成了 $1$。通过按位与上 $s$，可以将那些多余的 $1$ 与 $0$ 而抵消。

可以发现其复杂度为 $O(2^{\operatorname{popcount}(n)})$。

4. 考虑枚举 $\{0,1,2, \cdots, n-1 \}$ 的所有子集的所有子集，求复杂度？

A: 根据问题 3，枚举方法显然：

for (int i = 0; i < (1 << n); i++) {
	for (int j = i; j; j = (j - 1) & i);
}

复杂度为 $O(3^n)$。

:::success[证明]

我们根据组合数学知识来推导一下。考虑枚举每个子集中大小为 $i$ 的子集个数，则总数为

$$\sum_{i=0}^{n-1} C_n^i 2^i=\sum_{i=0}^{n-1} C_n^i 2^i 1^{n-i}=(1+2)^n-1=O(3^n) $$

这里我们逆用了二项式定理。

:::

如果直接暴力复杂度为 $O(4^n)$，而这个低复杂度做法是状压 dp 的常用技巧。

01-Trie

字符上的 Trie 属于字符串算法，而二进制上的 Trie 是解决异或问题的有力数据结构。

先介绍 Trie 树，其中文名为字典树，是一棵边带权的叶向树。借用 OI-Wiki 的图：

可以发现，Trie 树通过把相同的字符串前缀压到一起，实现节省复杂度的目的。而如果字符集为 $\{0,1\}$，就叫做 01-Trie，下面我们来介绍 01-Trie 维护异或和时的操作。

插入 & 删除

由于维护的是异或和，只需知道每一位上 $0/1$ 的奇偶性。故节点需要维护以下三个数组：

• ch[0/1][x]：维护节点 $x$ 的左 / 右儿子；
• w[x]：维护 $x$ 子树权值的数目。当然这里直接维护奇偶性就行了。
• xorv[x]：维护 $x$ 子树的整体异或和。

由此可以写出 01-Trie 的上传操作：

:::info[实现]

inline void pushup(int rt) {
    w[rt] = xorv[rt] = 0;
    if (ch[0][rt]) {
        w[rt] += w[ch[0][rt]];
        xorv[rt] ^= xorv[ch[0][rt]] << 1;
    }
    if (ch[1][rt]) {
        w[rt] += w[ch[1][rt]];
        xorv[rt] ^= (xorv[ch[1][rt]] << 1) | (w[ch[1][rt]] & 1);
    }
}

:::

插入删除是平凡的，将数二进制拆分后在遍历路径中更新对应信息即可。

:::info[实现]

inline int newnode() {
    cnt++;
    ch[1][cnt] = ch[0][cnt] = w[cnt] = xorv[cnt] = 0;
    return cnt;
}
void insert(int& rt, const T& x, int dep) {
    if (!rt) rt = newnode();
    if (dep > H) return w[rt]++, void();
    insert(ch[x & 1][rt], x >> 1, dep + 1);
    pushup(rt);
}

void remove(int rt, const T& x, int dep) {
    if (dep > H) return w[rt]--, void();
    remove(ch[x & 1][rt], x >> 1, dep + 1);
    pushup(rt);
}

:::

全局加一

一个神奇操作。考虑二进制下如何加一：

10101 + 1 = 10110
100000010111111 + 1 = 100000011000000

只需要找到最低位的 $0$，将其变为 $1$，然后把后面的所有 $1$ 置 $0$ 即可。放到 Trie 上，直接交换左右儿子并沿交换后 $0$ 的权值边向下递归即可。

:::info[实现]

void add1(int rt) {
    swap(ch[0][rt], ch[1][rt]);
    if (ch[0][rt]) add1(ch[0][rt]);
    pushup(rt);
}

:::

合并

没错，这神奇玩意还能合并。如果你学过线段树合并或者 FHQ-Treap 的话，这个东西相当好理解。

先判掉 $x,y$ 是空树的情况。直接把 $b$ 的信息放到 $a$ 上，然后递归合并左右儿子即可。

:::info[实现]

int merge(int a, int b) {
    if (!a || !b) return a ? a : b;
    w[a] += w[b], xorv[a] ^= xorv[b];
    ch[0][a] = merge(ch[0][a], ch[0][b]), ch[1][a] = merge(ch[1][a], ch[1][b]);
    return a;
}

:::

至此我们实现了一个支持插入 / 删除，全局加一，合并，全局异或和的数据结构。自己造的 板子题。

例题

P9451 [ZSHOI-R1] 新概念报数

分类讨论。设 $\operatorname{popcount}(a)=p$，则：

1. 若 $p \ge 3$，报告无解；
2. 若 $p \le 1$，直接输出 $a+1$，显然这样 $\operatorname{popcount(a+1)} \le 2$。
3. 若 $p=2$，找到 $a$ 二进制下最右侧的 $01$，然后改为 $10$ 即可。回顾一下问题 1，发现所求就是 $a+\operatorname{lowbit(a)}$。

:::info[代码]

uint64_t a;

void _main() {
	cin >> a;
	int p = __builtin_popcountll(a);
	if (p >= 3) return cout << "No,Commander\n", void();
	if (p <= 1) cout << a + 1 << '\n';
	else cout << a + (a & -a) << '\n';
}

:::

AT_abc365_e [ABC365E] Xor Sigma Problem

写过题解，复述一波：

显然 $a \oplus b \oplus b =a$，所以考虑记录一个 $pre$ 数组记录前缀异或和。

则

$$\begin{aligned} \sum_{i=1}^{i<n} \sum_{j=i+1}^{j\le n} \bigoplus_{k=i}^{k \le j} a_k &=\sum_{i=1}^{i\le n} \sum_{j=i}^{j\le n} \bigoplus_{k=i}^{k \le j} a_k - \sum_{i=1}^{i\le n} a_i \\ &= \sum_{i=1}^{i\le n} \sum_{j=i}^{j\le n} pre_{i} \oplus pre_{j} - \sum_{i=1}^{i\le n} a_i \end{aligned} $$

其中 $\sum_{i=1}^{i\le n} a_i$ 可以 $O(n)$ 计算，重点是计算前面这部分。

考虑把每个数按二进制拆分，逐位记录贡献，统计异或后二进制位为 $1$ 的贡献。

$\sum_{i=1}^{i\le n} \sum_{j=i}^{j\le n} pre_{i} \oplus pre_{j}$ 的意思是两两异或，所以可以用乘法原理，枚举二进制位 $d$，再设 $pre$ 中有 $s_0$ 个二进制第 $d$ 位为 $0$ 的，有 $s_1$ 个二进制第 $d$ 位为 $1$ 的，枚举前缀异或 $j$，第 $i$ 位贡献为 $2^i s_{1-pre_j}$。

时间复杂度 $O(n \log w)$。

:::info[代码]

const int N = 2e5 + 5;
int n, a[N], pre[N];

void _main() {
	cin >> n;
	long long tot = 0;
	for (int i = 1; i <= n; i++) cin >> a[i], tot += a[i], pre[i] = pre[i - 1] ^ a[i];
	long long res = 0;
	for (int i = 27; i >= 0; i--) {
		int s[2] = {0, 0};
		for (int j = 1; j <= n; j++) {
			int u = pre[j - 1] >> i & 1, v = pre[j] >> i & 1;
			s[u]++, res += (1LL << i) * s[v ^ 1];  
		}
	}
	cout << res - tot;
}

:::

这个题代表了一类位运算问题的套路，就是按位考虑贡献。

UVA11825 Hackers' Crackdown

状压 dp 是位运算的经典应用。首先我们预处理出来每台电脑能瘫痪的二进制状态 $s_i$，再考虑所有状态的并集 $c$，设 $dp_{s}$ 表示状态 $s$ 能够瘫痪多少服务，考虑使用子集枚举，对全集 $s_1$ 枚举子集 $s_2$，则 $dp_{s_1 } \gets dp_{s_2-s_1}+1$，复杂度 $O(3^n)$。

:::info[代码]

const int N = 16;
int n, m, a, s[N], c[1 << N], dp[1 << N];

void _main() {
	int kase = 0;
	while (cin >> n, n) {
		kase++;
		for (int i = 0; i < n; i++) {
			cin >> m;
			s[i] = 1 << i;
			while (m--) cin >> a, s[i] |= 1 << a;
		}
		memset(c, 0, sizeof(c)), memset(dp, 0, sizeof(dp));
		for (int i = 0; i < (1 << n); i++) {
			for (int j = 0; j < n; j++) {
				if (i >> j & 1) c[i] |= s[j]; 
			}
		}
		for (int i = 0; i < (1 << n); i++) {
			for (int j = i; j; j = (j - 1) & i) {
				if (c[j] == (1 << n) - 1) dp[i] = max(dp[i], dp[i - j] + 1);
			}
		}
		cout << "Case " << kase << ": " << dp[(1 << n) - 1] << '\n';
	}
} 

:::

P4310 绝世好题

$O(n^2)$ 暴力 dp 显然。就是设 $dp_i$ 表示以 $a_i$ 结尾的子序列的最大长度，则枚举满足 $a_i \& a_j \ne 0$ 的 $j$ 有

$$dp_i=\max_{j<i} \{dp_j+1\}$$

考虑位运算经典套路拆位。观察 $a_i \& a_j \ne 0$ 这个条件，发现只要 $i,j$ 在二进制下有一个相同位的 $1$ 就能转移。那么我们枚举二进制位 $j$，设 $dp_j$ 表示 $j$ 位为 $1$ 时的最大长度。若 $a_i$ 在二进制下的第 $j$ 位不为 $0$，则有转移

$$dp_j=\max dp_{j'}+1$$

这里 $j'$ 是另一个二进制位，由它转移而来即可。一个数 $a_i$ 可以被其二进制位的 $dp$ 转移，再转移到它二进制位的 $dp$ 值上。比较抽象，可以看代码理解。复杂度 $O(\log w)$。

:::info[代码]

const int N = 1e5 + 5;
int n, a[N], dp[40];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) {
		int mx = 0;
		for (int j = 0; j <= 31; j++) {
			if (a[i] >> j & 1) mx = max(mx, dp[j]);
		}
		for (int j = 0; j <= 31; j++) {
			if (a[i] >> j & 1) dp[j] = max(dp[j], mx + 1);
		}
	}
	cout << *max_element(dp, dp + 32);
}

:::

P10471 最大异或对 The XOR Largest Pair

感觉是 01-Trie 最经典的应用。先全部插入到 Trie 上，然后依次枚举每个数，找这个数能够形成的最大异或对。根据异或性质，我们贪心来取，每次尽量选不一样的数位遍历 01-Trie 即可。

:::info[代码]

const int N = 2e6 + 5;
int n, a[N];
int cnt = 1, ch[2][N];

void insert(int x) {
	int cur = 1;
	for (int i = 31; i >= 0; i--) {
		int p = x >> i & 1;
		if (!ch[p][cur]) ch[p][cur] = ++cnt;
		cur = ch[p][cur];
	}
}
int query(int x) {
	int cur = 1, res = 0;
	for (int i = 31; i >= 0; i--) {
		int p = x >> i & 1;
		if (!ch[p ^ 1][cur]) cur = ch[p][cur];
		else cur = ch[p ^ 1][cur], res += (1 << i);
	} return res;
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i], insert(a[i]);
	int res = 0;
	for (int i = 1; i <= n; i++) res = max(res, query(a[i]));
	cout << res;
}

:::

P4551 最长异或路径

好像没有头绪。记根节点到 $u$ 点的路径异或和为 $s_u$，推波式子：

$$\begin{aligned} e_u \oplus \cdots \oplus e_v &= e_u \oplus \cdots \oplus e_{lca(u,v)} \oplus e_v \oplus \cdots \oplus e_{lca(u,v)} \\ &= e_1 \oplus \cdots \oplus e_{lca(u,v)} \oplus \cdots \oplus e_u \oplus e_1 \oplus \cdots \oplus e_{lca(u,v)} \oplus \cdots \oplus e_v\\ &=s_u \oplus s_v \end{aligned} $$

这里利用了异或性质 $a \oplus a=0$，从根节点到 $lca(u,v)$ 这段路径异或两次就是没有异或。于是这题转化为上题。

P6018 [Ynoi2010] Fusion tree

我们发现操作 1 & 3 都是相邻点的操作，不好在树上维护，因此我们统一维护所有点儿子的异或信息，单独处理父亲。然后用 01-Trie 来维护即可，对每个点打个标记维护增加量。单独处理的时候，先删除再插入即可，具体看代码。

:::info[代码]

const int N = 5e5 + 5;
int tot = 0, head[N];
struct Edge {
	int next, to;
} edge[N << 1];
inline void add_edge(int u, int v) {
	edge[++tot].next = head[u], edge[tot].to = v, head[u] = tot;
}

#define ls (ch[0][rt])
#define rs (ch[1][rt])
int cnt, w[N * 21], xorv[N * 21], ch[2][N * 21];
int newnode() {
	cnt++;
	ch[1][cnt] = ch[0][cnt] = w[cnt] = xorv[cnt] = 0;
	return cnt;
} void pushup(int rt) {
	w[rt] = xorv[rt] = 0;
	if (ls) w[rt] += w[ls], xorv[rt] ^= xorv[ls] << 1;
	if (rs) w[rt] += w[rs], xorv[rt] ^= (xorv[rs] << 1) | (w[rs] & 1);
} void insert(int& rt, int x, int dep = 0) {
	if (!rt) rt = newnode();
	if (dep > 20) return w[rt]++, void();
	insert(ch[x & 1][rt], x >> 1, dep + 1), pushup(rt);
} void remove(int rt, int x, int dep = 0) {
	if (dep > 20) return w[rt]--, void();
	remove(ch[x & 1][rt], x >> 1, dep + 1), pushup(rt);
} void add1(int rt) {
	if (!rt) return;
	swap(ls, rs), add1(ls), pushup(rt);
} 

int n, q, u, v, a[N], opt, x, y;
int fa[N], rt[N], tag[N];

void dfs(int u, int f) {
	for (int j = head[u]; j != 0; j = edge[j].next) {
		int v = edge[j].to;
		if (v == f) continue;
		fa[v] = u, dfs(v, u);
	}
}

void change(int x, int c) {   // 单独处理节点x的权值
	if (x != 1) remove(rt[fa[x]], a[x] + tag[fa[x]]);
	a[x] += c;
	if (x != 1) insert(rt[fa[x]], a[x] + tag[fa[x]]);
}

void _main() {
	cin >> n >> q;
	for (int i = 1; i < n; i++) {
		cin >> u >> v;
		add_edge(u, v), add_edge(v, u);
	} dfs(1, -1);
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 2; i <= n; i++) insert(rt[fa[i]], a[i]);
	while (q--) {
		cin >> opt >> x;
		if (opt == 1) {
			tag[x]++, add1(rt[x]);  // 子树全局加1
			if (x != 1) change(fa[x], 1);
		} else if (opt == 2) {
			cin >> y, change(x, -y);
		} else if (opt == 3) {
			if (x != 1) {
				if (fa[x] != 1) cout << (xorv[rt[x]] ^ (a[fa[x]] + tag[fa[fa[x]]])) << '\n';
				else cout << (xorv[rt[x]] ^ a[fa[x]]) << '\n';
			} else {
				cout << xorv[rt[x]] << '\n';
			}
		}
	}
}

:::

P6623 [省选联考 2020 A 卷] 树

思考 $val(x)$ 的意义，可以发现一个暴力，就是将子树内的点权全部加 $1$ 后再异或起来贡献到父亲，是一个类似树形 dp 的思想。具体地，对于儿子 $v$ 的 $val_v =a_1 \oplus a_2 \oplus \cdots \oplus a_k$，则贡献为 $(a_1+1) \oplus (a_2+1) \oplus \cdots \oplus (a_k+1)$，复杂度 $O(n^2)$。

考虑在在每个节点建立一棵 01-Trie，对儿子的 Trie 作合并并全局加一，然后把自己的点权放进去。

考虑复杂度。Trie 的合并操作当且仅当两棵 Trie 存在相同元素时产生 $O(\log n)$ 复杂度。设其出现 $x$ 次，总合并次数 $\sum x = n$，因此复杂度为严格 $O(n \log n)$。

:::info[代码]

const int N = 6e5 + 5;
int tot, head[N];
struct Edge {
	int next, to;
} edge[N];
inline void add_edge(int u, int v) {
	edge[++tot].next = head[u], edge[tot].to = v, head[u] = tot;
}

int n, a[N], f;

#define ls (ch[0][rt])
#define rs (ch[1][rt])
int cnt, w[N * 20], xorv[N * 20], ch[2][N * 20];
int newnode() {
	cnt++;
	ch[1][cnt] = ch[0][cnt] = w[cnt] = xorv[cnt] = 0;
	return cnt;
} void pushup(int rt) {
	w[rt] = xorv[rt] = 0;
	if (ls) w[rt] += w[ls], xorv[rt] ^= xorv[ls] << 1;
	if (rs) w[rt] += w[rs], xorv[rt] ^= (xorv[rs] << 1) | (w[rs] & 1);
} void insert(int& rt, int x, int dep = 0) {
	if (!rt) rt = newnode();
	if (dep > 20) return w[rt]++, void();
	insert(ch[x & 1][rt], x >> 1, dep + 1), pushup(rt);
} void add1(int rt) {
	if (!rt) return;
	swap(ls, rs), add1(ls), pushup(rt);
} int merge(int a, int b) {
	if (!a || !b) return a ? a : b;
	w[a] += w[b], xorv[a] ^= xorv[b];
	ch[0][a] = merge(ch[0][a], ch[0][b]), ch[1][a] = merge(ch[1][a], ch[1][b]);
	return a;
}

int rt[N];
long long ans;
void dfs(int u) {
	for (int j = head[u]; j != 0; j = edge[j].next) {
		int v = edge[j].to;
		dfs(v), rt[u] = merge(rt[u], rt[v]);
	}
	add1(rt[u]), insert(rt[u], a[u]);
	ans += xorv[rt[u]];
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 2; i <= n; i++) cin >> f, add_edge(f, i);
	dfs(1); cout << ans;
} 

:::

AT_apc001_f XOR Tree

很神仙的一个题。

化边权为点权，把每个点的点权定义为其所连的边的边权异或和。此时再思考路径异或，发现因为 $a \oplus x \oplus x=a$，除了路径端点异或上一个 $x$，其他点点权不变。至此，题目转化为：

给定一个数组，每次将两个数将他们异或上同一个数，求最小操作次数使得数组所有数变为 $0$。

然而这个东西好像还是不可做。于是我们关注数据范围发现 $a_i \le 15$。我们先把权值相同的点两两抵消，那么剩下的是最多 $15$ 个互不相同的数字。

考虑状压 dp，设 $dp_{s}$ 表示以 $s$ 为状态的二进制集合全部消除的最小操作次数。当且仅当 $s$ 内数字异或和为 $0$ 时，$s$ 才能消掉。考虑转移，我们把 $s$ 拆成两个子集 $s_1,s_2$，且 $s_1,s_2$ 异或和均为 $0$，则两个子集直接合并就能减少一次操作。其实就是 Floyd 的思想。复杂度 $O(n+3^{V})$。

:::info[代码]

const int N = 1e5 + 5, M = 1 << 15;
int n, u, v, w, a[N], xorv[M + 5], cnt[20], dp[M + 5];

void _main() {
	cin >> n;
	for (int i = 1; i < n; i++) {
		cin >> u >> v >> w; u++, v++;
		a[u] ^= w, a[v] ^= w;
	}
	for (int i = 1; i <= n; i++) cnt[a[i]]++;
	int res = 0, fin = 0;
	for (int i = 1; i <= 15; i++) {
		res += cnt[i] / 2;
		if (cnt[i] & 1) fin |= 1 << (i - 1);  // 消不完
	}
	
	for (int i = 1; i < M; i++) {
		for (int j = 1; j <= 15; j++) {
			if (i >> (j - 1) & 1) xorv[i] ^= j;
		}
	}
	for (int i = 1; i < M; i++) {
		dp[i] = __builtin_popcount(i) - 1;
		if (xorv[i]) continue;
		for (int j = (i - 1) & i; j; j = (j - 1) & i) {
			if (xorv[j]) continue;
			dp[i] = min(dp[i], dp[j] + dp[i ^ j]);
		}
	}
	cout << res + dp[fin];
} 

:::

分数规划

分数规划一般与其他算法一起出现，比如：

• 与 01 背包结合，称为最优比率背包；
• 与最小生成树结合，称为最优比率生成树；
• 与最短路结合，称为最优密度路径；
• 与 SPFA 判负环结合，称为最优比率环；
• 与网络流结合，称为最优密度子图。

模型

分数规划的基本模型是：有 $n$ 个物品，每种物品有两个权值 $a,b$，选出若干个最大化或最小化 $\dfrac{\sum a} {\sum b}$。

最常见的模型里每种物品只有选与不选两种可能，因而又被称作 01-分数规划。

解法

最值问题且满足单调性，二分启动。以最大值为例，我们二分答案 $mid$，则

由

$$\dfrac{\sum a_i} {\sum b_i} > mid$$

可得

$$\sum a_i - mid \times \sum b_i > 0$$

即

$$\sum (a_i-mid \times b_i) > 0$$

由此得到二分的判定式。在分数规划的问题中，我们需要用其他方法求出 $\sum (a_i-mid \times b_i)$ 的最值并与 $0$ 比较。

例题

最大密度子图板子是 UVA1389 Hard Life，但是要用到笔者不太熟的网络流知识，这里就不讲了。

U581184 【模板】01-分数规划

自己造的板子。二分不变，可以贪心地去选，当且仅当 $a_i-mid \times b_i \ge 0$ 时我们才选这个物品。分数规划结合贪心。

:::info[代码]

const int N = 1e6 + 5;
int n, a[N], b[N];
const double eps = 1e-12;

inline bool check(double x) {
	double res = 0;
	for (int i = 1; i <= n; i++) res += max(a[i] - x * b[i], 0.0);
	return res > 0;
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
	double l = 0.0, r = 5e9;
	while (r - l > eps) {
		double mid = (l + r) / 2;
		if (check(mid)) l = mid;
		else r = mid;
	}
	cout << fixed << setprecision(12) << l;
}

:::

P4377 [USACO18OPEN] Talent Show G

仔细审题可以发现，这题等价于上面的模型，加入一个 $\sum b_i \ge W$ 的限制。

$\sum b_i \ge W$ 可以想到背包的容量，于是以 $b_i$ 为重量，$a_i-mid \times b_i$ 为体积跑 01 背包即可。如果不会 01 背包推荐我的背包笔记。复杂度 $O(nw \log V)$。分数规划结合 01 背包。

:::info[代码]

const int N = 1e5 + 5;

long long n, w, a[N], b[N];
const double eps = 1e-8;

double dp[N];
inline bool check(double x) {
	for (int i = 1; i <= w; i++) dp[i] = -1e9;
	for (int i = 1; i <= n; i++) {
		for (int j = w; j >= 0; j--) {
			dp[min(w, j + b[i])] = max(dp[min(w, j + b[i])], dp[j] + a[i] - x * b[i]);
		}
	} return dp[w] > 0;
}

void _main() {
	cin >> n >> w;
	for (int i = 1; i <= n; i++) cin >> b[i] >> a[i];
	double l = 0.0, r = 1e9;
	while (r - l > eps) {
		double mid = (l + r) / 2;
		if (check(mid)) l = mid;
		else r = mid;
	} cout << (long long) (1000 * l + eps);
}

:::

U589727 最优比率生成树

还是二分，接下来我们以 $a_i-mid \times b_i$ 为边权跑最小生成树，判断边权和是否大于 $0$ 即可。注意本题是完全图，用 prim 跑最小生成树更优。分数规划结合最小生成树。

:::info[代码]

const int N = 1005;
int tot = 0, head[N];
int val[N][N], cost[N][N];
double w[N][N];

int n, m, u, v, x, y;
const double eps = 1e-4;

bool vis[N];
double dis[N];
inline bool check(double x) {
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) w[i][j] = x * cost[i][j] - val[i][j];
	}
	memset(vis, 0, sizeof(vis)), fill(dis + 1, dis + n + 1, -1e9);
	dis[1] = 0; 
	for (int i = 1; i < n; i++) {
		int x = 0;
		for (int j = 1; j <= n; j++) {
			if (!vis[j] && (x == 0 || dis[j] > dis[x])) x = j;
		}
		vis[x] = true;
		for (int j = 1; j <= n; j++) {
			if (!vis[j]) dis[j] = max(dis[j], w[x][j]);
		}
	}
	double res = 0;
	for (int i = 2; i <= n; i++) res += dis[i];
	return res > 0;
}

void _main() {
	cin >> n;
	m = n * (n - 1) / 2;
	double l = 0.0, r = 5e6;
	for (int i = 1; i <= m; i++) {
		cin >> u >> v >> x >> y; 
		val[u][v] = val[v][u] = x;
		cost[u][v] = cost[v][u] = y;
	}
	while (r - l > eps) {
		double mid = (l + r) / 2;
		if (check(mid)) r = mid - eps;
		else l = mid + eps;
	} cout << fixed << setprecision(2) << l;
}

:::

P3199 [HNOI2009] 最小圈

人话就是求一个环 $C$ 使得 $\dfrac{\sum_{e \in C} w_e}{|C|}$ 最小。还是二分，这题 $b_i=1$，所以以 $a_i-mid$ 为边权。因为我们只需要判最小环是否小于 $0$，所以用 SPFA 判负环即可。分数规划结合 SPFA 判负环。

:::info[代码]

const int N = 1e4 + 5;
const double eps = 1e-10;

int tot = 0, head[N];
struct Edge {
	int next, to;
	double dis;
} edge[N << 1];
inline void add_edge(int u, int v, double w) {
	edge[++tot].next = head[u], edge[tot].to = v, edge[tot].dis = w, head[u] = tot;
}
int n, m, u, v; double w;

deque<int> q;
double dis[N]; int cnt[N];
bitset<N> vis;

inline bool spfa(int s, double x) {
	for (int i = 1; i <= n; i++) dis[i] = 1e9;
	q.clear(), memset(cnt, 0, sizeof(cnt)), vis.reset();
	q.emplace_back(s), dis[s] = 0, vis[s] = 1, cnt[s] = 1;
	while (!q.empty()) {
		int u = q.front(); q.pop_front(), vis[u] = 0;
		if (!q.empty() && dis[q.front()] > dis[q.back()]) swap(q.front(), q.back());
		for (int j = head[u]; j != 0; j = edge[j].next) {
			int v = edge[j].to;
			double w = edge[j].dis - x;
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if (++cnt[v] >= n) return true;
				if (vis[v]) continue;
				vis[v] = 1, q.emplace_back(v);
				if (!q.empty() && dis[q.front()] > dis[q.back()]) swap(q.front(), q.back());
			}
		}
	}
	return false;
}

void _main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) cin >> u >> v >> w, add_edge(u, v, w);
	double l = -1e7, r = 1e7; 
	while (r - l > eps) {
		double mid = (l + r) / 2;
		if (spfa(1, mid)) r = mid;
		else l = mid;
	} cout << fixed << setprecision(8) << l;
}

:::

但是这题即使用 SLF+swap 的 SPFA 也只有 90pts，使用玄学的 DFS-SPFA 可以水过。

:::warning[警告]

DFS-SPFA 使用必须慎重，其最差复杂度为指数级。

:::

:::info[代码]

double dis[N];
bool vis[N];

bool dfs(int u, double x) {
	vis[u] = true;
	for (int j = head[u]; j != 0; j = edge[j].next) {
		int v = edge[j].to; double w = edge[j].dis - x;
		if (dis[v] > dis[u] + w) {
			dis[v] = dis[u] + w;
			if (vis[v] || dfs(v, x)) return true;
		}
	} return vis[u] = false; 
}
inline bool check(double x) {
	fill(dis + 1, dis + n + 1, 0.0), fill(vis + 1, vis + n + 1, false);
	for (int i = 1; i <= n; i++) {
		if (dfs(i, x)) return true;
	} return false;
}

:::

P1730 最小密度路径

还是分数规划的模型，二分起手，这题 $a_i=w,b_i=1$，然后以 $w-mid$ 为边权从 $u$ 到 $v$ 跑 SPFA 最短路即可。这题是最小值，所以就是判最短路小于 $0$。因为这题 $q$ 个询问只有 $O(n^2)$ 个本质不同，打个记忆化即可。分数规划结合最短路。

:::info[代码]

const int N = 1005;
const double eps = 1e-5;
int n, m, u, v, w, q;
double ans[N][N];

int tot = 0, head[N];
struct Edge {
	int next, to;
	double dis;
} edge[N << 1];
inline void add_edge(int u, int v, double w) {
	edge[++tot].next = head[u], edge[tot].to = v, edge[tot].dis = w, head[u] = tot;
}
double dis[N];
bool vis[N];
inline bool spfa(int s, int t, double x) {
	fill(dis + 1, dis + n + 1, 1e9), memset(vis, 0, sizeof(vis));
	queue<int> q;
	q.emplace(s), dis[s] = 0, vis[s] = true;
	while (!q.empty()) {
		int u = q.front(); q.pop();
		vis[u] = false;
		for (int j = head[u]; j != 0; j = edge[j].next) {
			int v = edge[j].to; double w = edge[j].dis - x;
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if (vis[v]) continue;
				vis[v] = true, q.emplace(v);
			}
		}
	} return dis[t] < 0;
}	

void _main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		cin >> u >> v >> w;
		add_edge(u, v, w);
	} cin >> q;
	while (q--) {
		cin >> u >> v;
		if (ans[u][v] != 0) {
			if (ans[u][v] == -1) cout << "OMG!\n"; 
			else cout << fixed << setprecision(3) << ans[u][v] << '\n';
			continue;
		}
		double l = 0.0, r = 1e5, res = -1;
		while (r - l > eps) {
			double mid = (l + r) / 2.0;
			if (spfa(u, v, mid)) r = mid, res = r;
			else l = mid;
		}
		if (res == -1) ans[u][v] = -1, cout << "OMG!\n";
		else cout << fixed << setprecision(3) << (ans[u][v] = res) << '\n';
	}
} 

:::

高斯消元

步骤

高斯消元是用来解线性方程组或异或方程组的一种算法。下面先以线性方程组

$$\left\{\begin{matrix} 2x+y-z=8 \\ -3x-y+2z=-11 \\ -2x+y+2z=-3 \end{matrix}\right. $$

为例说明。

我们通过三种基本操作来消元（这些操作保证方程组的解不会改变）：

1. 交换方程位置：例如，把第一个方程和第二个方程互换。
2. 乘以非零常数：例如，将某个方程两边同时乘以 2 或 -3（但不能乘以 0）。
3. 添加一个方程的倍数：例如，把第一个方程的 2 倍加到第二个方程上。

高斯消元有两个步骤，第一步为前向消元（即简化方程组），第二部为回代求解。

前向消元

这一步消元后，方程组变成“三角形”形式，即每个方程比前一个少一个变量。我们从上到下逐个变量处理。

• 第一步：在方程 2 和 3 中消去 $x$
  • 把方程 1 作为最后留下 $x$ 的那个方程，因为 $x$ 的系数不为 $0$。
  • 处理方程 2：计算一个倍数使得 $x$ 的系数为 $0$。倍数 $m=\dfrac{-3}{2}=-1.5$，也就是用方程 2 的 $x$ 系数去除以方程 1 的系数。则方程 2 化为 $(-3x-y+2z)-m(2x+y-z)=0.5y+0.5z=-11-8m=1$。为方便讲解这里化为 $y+z=2$。
  • 处理方程 3：仿照上例，将方程 3 的 $x$ 系数化为 $0$。此时，$m=\dfrac{-2}{2}=-1$，方程 3 化为 $( -2x+y+2z)-m(2x+y-z)=2y+z=-3-8m=5$。
  • 现在方程组已经化为

$$\left\{\begin{matrix} 2x+y-z=8 \\ y+z=2 \\ 2y+z=5 \end{matrix}\right. $$

• 第二步：在方程 3 中消去 $y$
  • 此步骤忽略方程 1，因为其存在 $x$ 项。
  • 把方程 2 作为最后留下 $y$ 的那个方程，因为 $y$ 的系数不为 $0$。
  • 处理方程 3：仿照上例，将方程 3 的 $y$ 系数化为 $0$。此时，$m=\dfrac{2}{1}=2$，方程 3 化为 $(2y+z)-m(y+z)=-z=5-2m=1$。
  • 现在方程组已经化为

$$\left\{\begin{matrix} 2x+y-z=8 \\ y+z=2 \\ -z=1 \end{matrix}\right. $$

至此，方程组已被化为“三角形”形式，最后一个方程可直接求得 $z=-1$。

回代求解

从最后一个方程开始，逐个求解变量，并代入前一个方程。

比如这里求得 $z=-1$，代入方程 2 得 $y=3$，再代进方程 1 中解得 $x=2$，所以方程组的解为

$$\left\{\begin{matrix} x=2 \\ y=3 \\ z=-1 \end{matrix}\right. $$

还可以考虑无解 / 无穷多解的情况。无解时，一条方程形如 $0x=c$，其中 $c$ 是不为 $0$ 的常数。而无穷多解则是 $0x=0$ 的形式。

代码上有很多细节，比如选择合适的顺序以减小浮点误差，交换方程等等。

模板

:::info[代码]

template <int N>
class GuassSolution {
private:
	int n, m;
	double a[N][N];
public:
	explicit GuassSolution(int _n) : n(_n), m(0) {}
	template <class T> void add(const T& it, double val) {
		for (int i = 0; i < n; i++) a[m][i] = it[i];
		a[m][n] = val, m++;
	}
	
	template <class T> int solve(T it, double eps = 1e-9) {  // 无解-1，唯一解0，无穷解1
		int ln = 0;
		for (int k = 0; k < n; k++) {  // 消去x_k
			int mx = ln;
			for (int i = ln + 1; i < m; i++) {
				if (abs(a[i][k]) > abs(a[mx][k])) mx = i;
			}  // 找最大系数，可以减小误差
			if (abs(a[mx][k]) < eps) continue;
			for (int j = 0; j <= n; j++) swap(a[ln][j], a[mx][j]);
			for (int i = 0; i < m; i++) {  // 在方程中消去x_k
				if (i == ln) continue;
				double x = a[i][k] / a[ln][k];  // 变系数
				for (int j = k; j <= n; j++) a[i][j] -= a[ln][j] * x;  // 加减消元
			}
			ln++;
		}
		if (ln < n) {  // 意味着有一条方程的左边为 0
			for (; ln < n; ln++) {
				if (abs(a[ln][n]) > eps) return -1;
			}
			return 1;
		}
		for (int i = 0; i < n; i++) it[i] = a[i][n] / a[i][i];  // 回代求解
		return 0;
	}
};

:::

显然可以看出复杂度为 $O(n^2m)$，其中 $n$ 为未知数的个数，$m$ 为方程的条数。

异或方程组

上述过程可以给出线性方程组的数值解法，而若方程形如

$$\left\{\begin{matrix} a_{1,1} x_1 \oplus a_{1,2} x_2 \oplus \cdots \oplus a_{1,n} x_n = v_1 \\ a_{2,1} x_1 \oplus a_{2,2} x_2 \oplus \cdots \oplus a_{2,n} x_n = v_2 \\ \cdots \\ a_{m,1} x_1 \oplus a_{m,2} x_2 \oplus \cdots \oplus a_{m,n} x_n = v_m \end{matrix}\right. $$

其中 $a_{i,i}, v_i \in \{0,1\}$，则仍然可以使用类似方法解决。具体地，因为异或有结合律、交换律，并且我们还不用乘除来改变系数，直接异或消元就行了。然而异或方程组会出现“自由元”，比如方程组

$$\left\{\begin{matrix} x_1 \oplus x_2 = 1 \\ x_2 \oplus x_3 = 1 \\ x_1 \oplus x_3 = 0 \end{matrix}\right. $$

与线性方程组不同，即使 $n$ 元有 $n$ 个方程也会多解。上述异或方程组逻辑上为：$x_1=x_3$ 且 $x_1 \ne x_2$。于是 $x_3$ 取 $0,1$ 都是可以的。对于这种自由元，我们只能全解完后 dfs 暴力求解。

可以用 bitset 优化，时间复杂度变为 $O(\dfrac{n^2m}{w})$。

例题

P2455 [SDOI2006] 线性方程组

高斯消元板子。

:::info[代码]

int n, a[N];
double x[N];

void _main() {
	cin >> n;
	GuassSolution<N> sol(n);
	for (int i = 1; i <= n; i++) {
		for (int i = 0; i <= n; i++) cin >> a[i];
		sol.add(a, a[n]);
	}
	int opt = sol.solve(x + 1);
	if (opt == -1) cout << -1;
	else if (opt == 1) cout << 0;
	else {
		for (int i = 1; i <= n; i++) {
			cout << 'x' << i << '=';
			if (abs(x[i]) > 1e-5) cout << fixed << setprecision(2) << x[i] << '\n';
			else cout << 0 << '\n';  // 这里不这样处理的话会出现 -0.00 的输出
		}
	}
}

:::

P4035 [JSOI2008] 球形空间产生器

好像这题沦落为退火板子了（

根据题意列方程，设球心为 $(x_1,x_2,x_3,\cdots,x_n)$，则

$$\forall 1 \le i \le n+1, \sum_{j=1}^{n} (a_{i,j}-x_j)^2=r^2 $$

定睛一看是二次方程。这里用到一个 trick，相邻两个方程作差，此时化为 $n$ 元一次方程组，满足

$$\forall 1 \le i \le n, \sum_{j=1}^{n} [{a_{i,j}}^2-{a_{i+1,j}}^2-2x_j(a_{i,j}-a_{i+1,j})]=0 $$

化成标准形式

$$\forall 1 \le i \le n, \sum_{j=1}^{n} 2x_j(a_{i,j}-a_{i+1,j})=\sum_{j=1}^{n}({a_{i,j}}^2-{a_{i+1,j}}^2) $$

于是就可以高斯消元解方程组了。

:::info[代码]

const int N = 100;
int n;
double a[N][N], b[N], x[N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 1; j <= n; j++) cin >> a[i][j];
	}
	GuassSolution<N> sol(n);
	for (int i = 1; i <= n; i++) {
		double v = 0;
		for (int j = 1; j <= n; j++) {
			b[j - 1] = 2.0 * (a[i][j] - a[i + 1][j]);
			v += a[i][j] * a[i][j] - a[i + 1][j] * a[i + 1][j];
		} sol.add(b, v);
	} sol.solve(x);
	for (int i = 0; i < n; i++) cout << fixed << setprecision(3) << x[i] << ' ';
}

:::

P2011 计算电压

请物竞生来应该能秒掉罢。

考虑用物理知识列方程，由基尔霍夫定律可得流入电流等于流出电流，且根据电压本质是电势差可得

$$\sum_{(j, i)} \dfrac{U_j-U_i}{R_{j,i}}=\sum_{(i,k)} \dfrac{U_i-U_k}{R_{i,k}} $$

用到了欧姆定律 $I=\dfrac{U}{R}$。意义是 $i$ 节点的入边贡献的电流等于出边的总电流，取并集

$$\sum_{(i,j)} \dfrac{U_j-U_i}{R_{i,j}}=0$$

这个式子最大的好处是化边权为点权且无需判断电流方向。

然后我们枚举点 $i$，若它直接连向电源，电压就是给出的值，否则枚举出边列方程，这样是一个 $n$ 元一次方程组，且主元系数均不为 $0$，故一定有解。可以发现复杂度为 $O(n^3+m)$。

:::info[代码]

const int N = 2e5 + 5;

int tot = 0, head[N];
struct Edge {
	int next, to; double dis;
} edge[N << 1];
inline void add_edge(int u, int v, double w) {
	edge[++tot].next = head[u], edge[tot].to = v, edge[tot].dis = w, head[u] = tot;
}

int n, m, k, q, u, v, num;
double val, h[N], U0[N], U[N];

void _main() {
	cin >> n >> m >> k >> q;
	GuassSolution<205> sol(n);
	for (int i = 1; i <= k; i++) cin >> u >> U0[u];
	for (int i = 1; i <= m; i++) {
		cin >> u >> v >> val;
		add_edge(u, v, val), add_edge(v, u, val);
	}
	for (int u = 1; u <= n; u++) {
		fill(h + 1, h + n + 1, 0);
		if (U0[u] > 0) {
			h[u] = 1, sol.add(h + 1, U0[u]);
		} else {
			for (int j = head[u]; j != 0; j = edge[j].next) {
				int v = edge[j].to; double w = edge[j].dis;
				h[v] += 1.0 / w, h[u] -= 1.0 / w;
			} sol.add(h + 1, 0);
		}
	}
	sol.solve(U + 1);
	while (q--) cin >> u >> v, cout << fixed << setprecision(2) << U[u] - U[v] << '\n';
}

:::

P2447 [SDOI2010] 外星千足虫

题意翻译：给出方程组

$$\left\{\begin{matrix} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n \equiv v_1 \pmod 2 \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n \equiv v_2 \pmod 2 \\ \cdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n \equiv v_m \pmod 2 \end{matrix}\right. $$

求方程组的解，并且求最少的方程条数使得方程组有唯一解。

思考一下模 $2$ 意义下的加法，发现这就是异或，于是第一问套用高斯消元即可。考虑第二问，显然至少要 $n$ 个方程才能解出 $n$ 元异或方程组，于是我们先解完 $n$ 个方程，若存在自由元就再加入新方程，直到有唯一解或者方程用完为止。使用 bitset 优化即可通过。

:::info[代码]

const int N = 2005;
int n, m; char c;
bitset<N> a[N];
int v[N], id[N];

int guass() {
	int cnt = 0;
	for (int k = 1; k <= n; k++) {
		int mx = m + 1;
		for (int i = k; i <= m; i++) {
			if (a[i][k] && id[mx] > id[i]) mx = i;
		}
		if (mx == m + 1) return -1;
		cnt = max(cnt, id[mx]);
		swap(a[k], a[mx]), swap(v[k], v[mx]), swap(id[k], id[mx]);
		for (int i = 1; i <= m; i++) {
			if (i != k && a[i][k]) a[i] ^= a[k], v[i] ^= v[k];
		}
	} return cnt;
}

void _main() {
	cin >> n >> m; 
	iota(id + 1, id + m + 2, 1);
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) cin >> c, a[i][j] = c ^ 48;
		cin >> c, v[i] = c ^ 48;
	}
	int h = guass();
	if (h == -1) return cout << "Cannot Determine", void();
	cout << h << '\n';
	for (int i = 1; i <= n; i++) cout << (v[i] ? "?y7M#\n" : "Earth\n");
}

:::